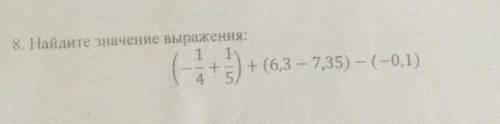
(−41+51)+(6,3−7,35)−(−0,1)
1) -\frac{1}{4} + \frac{1}{5} = -\frac{5}{20} + \frac{4}{20} = -\frac{1}{20} = -0,05−41+51=−205+204=−201=−0,05
2) 6,3 - 7,35 = -1,05
3) -0,05 + (-1,05) = -0,05 - 1,05 = -1,1
4) -1,1 - (-0,1) = -1,1 + 0,1 = -1
ответ : -1.
Пошаговое объяснение:
это правильно !
ответ: 3,4,5,6
Пошаговое объяснение:
Поскольку во всех перечисленных вариантах каждая цифра строго больше/меньше предыдущей, то все цифры в таких последовательностях различны, таким образом, общее количество последовательностей из n цифр от 0 до 9, где каждая цифра больше/меньше предыдущей ровно числу cпособов выбрать n различных цифр из 10-ти возможных, ибо существует ровно один упорядочить в порядке возрастания/убывания набор различных цифр.
Cравним различные значения количеств последовательностей для всех представленных вариантов.
1) Последовательностей из 9 цифр от 000000000 до 999999999 таких, что каждая цифра больше/меньше предыдущей:
Тут очевидно ровно 10 таких вариантов - число вариантов изъять одну цифру из десяти возможных.
2) Последовательностей из 6 или 4 цифр от 000000 до 999999 таких, что каждая цифра больше/меньше предыдущей:
Нетрудно убедиться, что выбрав некоторые 4 цифры от 0 до 10 останется ровно 10 - 4 = 6 цифр, таким образом, количества таких последовательностей для 4 и 6 цифр одинаковы, при этом очевидно, что в данных последовательностях число вариантов будет больше 10, ибо количество возможных изымаемых цифр будет больше одного.
Поэтому наибольшие величины находятся в пунктах: 3,4,5,6
Можно посчитать это наибольшее количество:
C(10,4) = C(10,6) = 10!/(4!*6!) = 210 (необязательно)
1)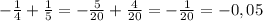
2) 6,3 - 7,35 = -1,05
3) -0,05 + (-1,05) = -0,05 - 1,05 = -1,1
4) -1,1 - (-0,1) = -1,1 + 0,1 = -1
ответ : -1.