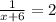Найдите корень уравнения. Я посмотрел ответы, будет -5,5. Каким образом можно получить этот
Пошаговое объяснение:
Нам нужно решить уравнение (2,5y - 4)(6y + 1,8) = 0.
Для этого мы рассмотрим и проанализируем заданное уравнение.
Наше уравнение представляет собой равенство в правой части которой стоит ноль, а в левой произведение двух скобок.
Известно, что произведение равно нулю, когда хотя бы один из множителей равен нулю.
Чтобы найти все корни уравнения приравняем каждый из множителей к нулю и решим полученные уравнения.
1) 2.5y - 4 = 0;
2.5y = 4;
y = 4 : 2.5;
y = 1.6;
2) 6y + 1.8 = 0;
6y = -1.8;
y = -1.8 : 6;
y = -0.3.
ответ: y = 1.6; y = -0.3.
1) -3 * (х - 4) = 5х - 12;
-3х + 12 = 5х - 12;
-3х - 5х = -12 - 12;
-8х = -24;
х = 24 / 8 = 3;
2) (16 - 5х) - (3 - 5х) = 6;
16 - 5х - 3 +5х = 6;
13 - 0х = 6; 3) 26 - 4х = 3х - 7 * (х - 3);
26 - 4х = 3х - 7х + 21; 4) -2 * (3 - 4х) + 5 * (2 - 1 , 6х) = 4;
-6 + 8х + 10 - 8х = 4;
-6 + 8х + 10 - 8х - 4 = 0;
-4х + 4х = 21 - 26;
Пошаговое объяснение:
Пошаговое объяснение:
Решенре на фотке............
.