2. Угол при основании равнобедренного треугольника АВС равен 32º, АВ -его боковая сторона, АМ- биссектриса треугольника. Найдите углы треугольника АВМ. (Рассмотрите два случая.)
1) ∠В=180º - 32º*2 = 116º
Так как АМ – биссектриса ∠ВАМ=32:2=16º
∠АМВ=180 – 116-16=48º
2) Из Δ АМС ∠ АМС= 180 – 32-16= 132º
∠АМВ и ∠АМС смежные, значит ∠АМВ=180-132=48º
∠В= 180º- ∠ВАМ -∠АМВ =180-48-16=116º
3. К прямой т проведены перпендикуляры АВ и СD. Докажите, что ∆ АВD=∆ CDB, если AD = BC.
АВ и СD перпендикуляры, значит ∠ ВDС и ∠ АВD =90 º . В четырехугольнике АВDС два угла прямоугольные, а диагонали равны AD = BC. Значит АВDС – прямоугольник. У прямоугольника противоположные стороны равны.
АВ=СD , AD = BC, ВD – общая сторона.
∆ АВD=∆ CDB по трем равным сторонам.
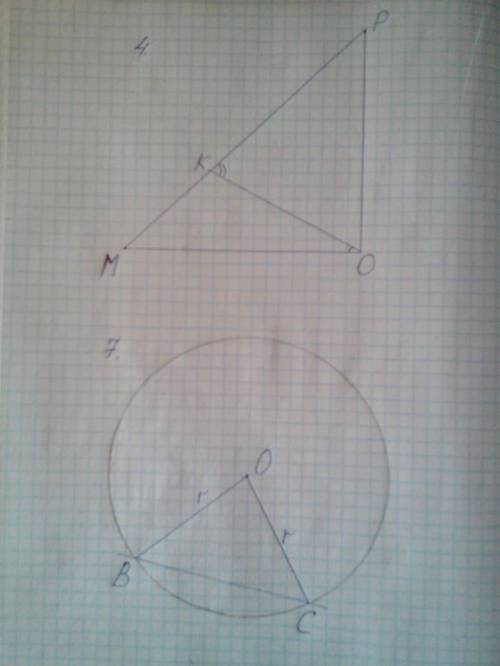
4. В равнобедренном прямоугольном треугольнике MOP на гипотенузе МP отмечена точка К. Известно, что ∠OKP в 4 раза больше, чем ∠МОК. Найдите углы треугольника МОК.
Δ МОК прямоугольный равнобедренный.
∠М=∠Р = 90º:2=45º
∠ОКР=4*∠МОК
Из теоремы о внешних углах ∠М= ∠ОКР-∠МОК
∠М= 4*∠МОК-∠МОК=3∠МОК
∠МОК = 45º:3=15º
∠ МКО=180º - 45º -15º = 120º
Или ∠МКО= 180º - 4*15º=120º
7. В окружности с центром О проведена хорда ВС. Найдите ∠OВС и ∠ВOС, если один из них на 36 º больше другого.
Δ ОВС равнобедренный ВО=ОС= r , значит прилежащие к основанию углы равны.
∠OВС=∠OСВ =хº
2х+х+36 =180
3х = 144
х = 48
∠OВС=∠OСВ =48º
∠ВOС= 48º+36º=84º

Шахматисты, занявшие четыре последних места, сыграли между собой 6 партий. Поэтому все вместе они набрали не меньше 6 очков.
Так как каждый игрок сыграл в турнире 7 партий, то победитель мог набрать максимум 7 очков. Поскольку победитель набрал больше очков, чем игрок, занявший второе место, то последний не мог набрать 6,5 очка, т.к. это означало бы, что у победителя было бы тогда 7 очков, т.е. он выиграл бы все партии, а у второго игрока было бы поражение. Значит игрок, занявший второе место набрал 6 очков.
Поэтому шахматисты, занявшие четыре последних места, набирали очки только во встречах друг с другом, а всем остальным участникам проиграли. Значит игрок, занявший третье место, выиграл у игрока, занявшего седьмое.
1)биссектриса делит угол пополам, в равнобедренном треугольнике высота медиана и биссектриса совпадают
2) Серединный перпендикуляр – это прямая, проходящая через середину отрезка перпендикулярно к нему
3)Все точки серединного перпендикуляра к отрезку равноудалены от концов этого отрезка
5)равнобедренный,прямоугольный,тупоугольный,остроугольный,правильный.
6)биссектриса это прямая проходящая через вершину угла и делящая его пополам.
7) взаимно противоположные