Пошаговое объяснение:
1) R1 «иметь один и тот же остаток от деления на 5»; M1 множество натуральных чисел.
2) R2 «быть равным»; M2 множество натуральных чисел.
3) R3 «жить в одном городе»; M3 множество людей.
4) R4 «быть знакомым»; M4 множество людей.
5) R5 {(a,b):(a-b) - чётное; M5 множество чисел {1,2,3,4,5,6,7,8,9}.
6) R6 {(a,b):(a+b) - чётное; M6 множество чисел {1,2,3,4,5,6,7,8,9}.
7) R7 {(a,b):(a+1) - делитель (a+b)} ; M7 - множество {1,2,3,4,5,6,7,8,9}.
8) R8 {(a,b):a - делитель (a+b),a≠1}; M8 - множество натуральных чисел.
9) R9 «быть сестрой»; M9 - множество людей.
10) R10 «быть дочерью»; M10 - множество людей.
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
пути.
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
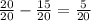
50 км =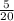 
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км = 
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
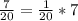
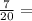10 км * 7 = 70 км.
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
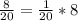
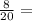10 км * 8 = 80 км.
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.
ответ: для ответа листайте ниже это чтобы не удалили
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m - любые действительные числа. Тогда
1) an am = an+m
2)
a
n
a
m
=
a
n
−
m
3) (an)m = anm
4) (ab)n = an bn
5)
(
a
b
)
n
=
a
n
b
n
6) an > 0
7) an > 1, если a > 1, n > 0
8) an < am, если a > 1, n < m
9) an > am, если 0< a < 1, n < m
В практике часто используются функции вида y = ax, где a - заданное положительное число, x - переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0,
a
≠
1
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0,
a
≠
1
, не имеет корней, если
b
≤
0
, и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 < a < 1.
Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х < 0 и |х| увеличивается, то график быстро приближается к оси Oх (но не пересекает её). Таким образом, ось Ох является горизонтальной асимптотой графика функции у = ax при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси Ох.
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х < 0 и |х| увеличивается, то график быстро поднимается вверх.
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0,
a
≠
1
, х — неизвестное. Это уравнение решается с свойства степени: степени с одинаковым основанием а > 0,
a
≠
1
равны тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде 8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
ответ х = 2
Решить уравнение 3х + 1 - 2 • 3x - 2 = 25
Вынося в левой части за скобки общий множитель 3х - 2, получаем 3х - 2(33 - 2) = 25, 3х - 2 • 25 = 25,
откуда 3х - 2 = 1, x - 2 = 0, x = 2
ответ х = 2
Решить уравнение 3х = 7х
Так как
7
x
≠
0
, то уравнение можно записать в виде
3
x
7
x
=
1
, откуда
(
3
7
)
x
=
1
, х = 0
ответ х = 0
Решить уравнение 9х - 4 • 3х - 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 - 4t - 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3х = 9, 3х = -5.
Уравнение 3х = 9 имеет корень х = 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
ответ х = 2
Пошаговое объяснение:ответ 18 в онлайнмектеп