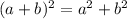 то это большое заблуждение!
то это большое заблуждение!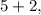 понятно, что
понятно, что 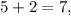 но мы не будем сразу возводить
но мы не будем сразу возводить 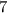 в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)
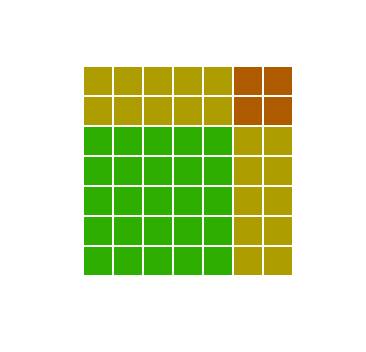
в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)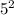 (это зелёный квадрат) и
(это зелёный квадрат) и 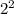 (это оранжевый квадрат), то мы не получим площадь квадрата со стороной
(это оранжевый квадрат), то мы не получим площадь квадрата со стороной 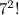 Чтобы получить правильную сумму
Чтобы получить правильную сумму 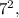 необходимо прибавить ещё два жёлтых прямоугольника с площадями
необходимо прибавить ещё два жёлтых прямоугольника с площадями 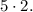
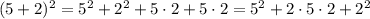 ;
;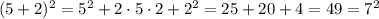 ;
;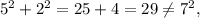 потому:
потому: 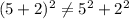 ;
;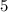 и
и 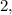 а для каких-то любых
а для каких-то любых  и
и 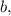 то получилось бы всё аналогично:
то получилось бы всё аналогично: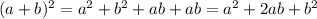 ;
; ;
;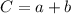 :
: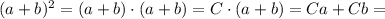
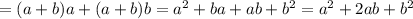 ;
;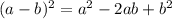 ;
;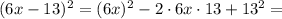
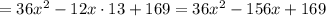 ;
;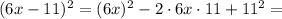
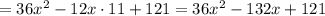 ;
;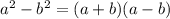 формула [2] ;
формула [2] ;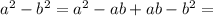
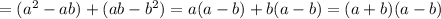 ;
;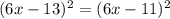 ;
;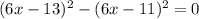 ;
;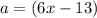 и
и 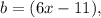 тогда:
тогда: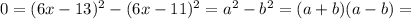
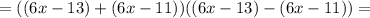
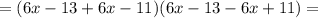
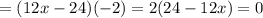 ;
;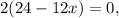 что возможно только если выражение в скобках равна нулю, т.е.:
что возможно только если выражение в скобках равна нулю, т.е.: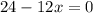 ;
;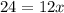 ;
;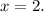
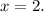
ответ:9²81
9³=729
9⁴=6561
3
Пошаговое объяснение:В конце числа 2019 стоит 9.
При многократном перемножении 9 на саму себя, в конце числа будет либо 1, либо 9.
Число 2019 нечетное, значит в конце выражения 2019^2019 будет стоять 9.
В конце числа 2018 стоит 8.
При многократном перемножении 8 на саму себя, в конце числа будут чередоваться цифры 8, 4, 2 и 6.
Цифра 8 в конце выражения появится, если степень числа кратна 5 или равна 1, цифра 4, если степень кратна 2, цифра 2, если степень кратна 3, цифра 6, если степень кратна 4.
Число 2018 кратно 2, поэтому в конце выражения 2018^2018 будет стоять 4.
Сумма чисел, в конце которых стоят 9 и 4 даст число, в конце которого стоит 3.