В полдень обе стрелки часов показывают на 12. Затем минутная стрелка сделает полный оборот, а часовая будет показывать 1 час. Пока минутная стрелка повернётся к 1(пройдёт 5 минут), часовая опять чуть-чуть убежит вперёд. Так что обе стрелки встретятся ещё раз через 1 час, 5 минут и ещё какое-то количество секунд.
А теперь строгие вычисления.
Угловая скорость часовой стрелки (полный оборот 360° за 12·60·60c)
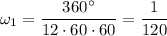 °/c
°/c
Угловая скорость минутной стрелки (полный оборот 360° за 60·60c)
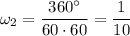 °/c
°/c
Пусть стрелки в следующий раз встретятся через время t, за которое минутная стрелка успеет сделать на целый оборот больше, чем часовая.
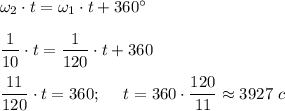
t = 3927 с = 65 мин 27 с
ответ: стрелки встретятся примерно через 1 час 5 минут 27 секунд
400≤18k≤1000
400/18≤k≤1000/18
Так как k целое, то округлим 400/18 до целого вверх, а 1000/18 до целого вниз. Получим: 23≤k≤55. Сумма чисел вида 18k при 23≤k≤55 равна 18*(23+...+55)=18*(23+55)/2*(55-23+1)=18*78/2*33=23166.
Теперь среди найденных чисел нужно вычесть сумму тех, которые делятся помимо 6 и 9 еще и на 13. НОК(18,13)=18*13=234. То есть это числа вида 234n, где n - целое. Найдем границы: 400≤234n≤1000,
400/234≤n≤1000/234
2≤n≤4
Сумма таких чисел равна 234*(2+3+4)=234*9=2106.
Из первой суммы вычтем вторую сумму и получим конечный результат:
23166-2106=21060.