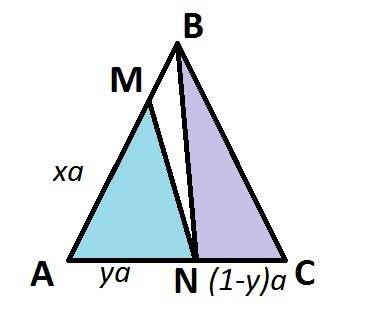
 . Обозначим отрезок AM как
. Обозначим отрезок AM как 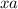 , где
, где ![x\in[0;1]](/tpl/images/0719/8692/13821.png) и отрезок AN как
и отрезок AN как 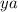 , где
, где ![y\in[0;1]](/tpl/images/0719/8692/d57b3.png) . Тогда сторона MB выразится как
. Тогда сторона MB выразится как 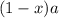 , а сторона NC выразится как
, а сторона NC выразится как 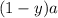 .
.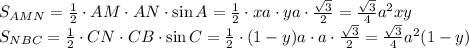
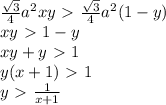
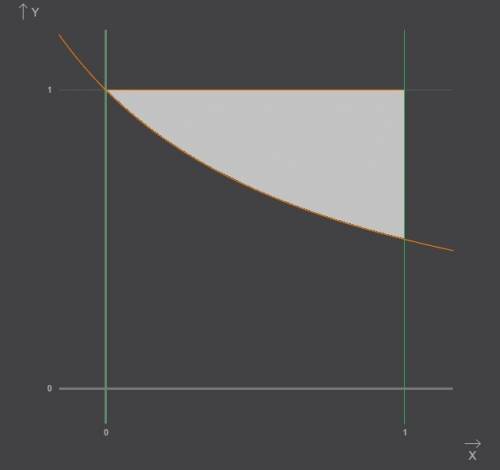
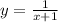 . Численно эта площадь равна искомой вероятности.
. Численно эта площадь равна искомой вероятности.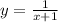 получается из графика функции
получается из графика функции 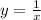 путем параллельного переноса на 1 единицу влево.
путем параллельного переноса на 1 единицу влево.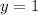 , снизу - графиком функции
, снизу - графиком функции 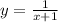 , слева и справа - прямыми
, слева и справа - прямыми 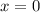 и
и 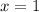 соответственно. Площадь такой фигуры определяется определенным интегралом
соответственно. Площадь такой фигуры определяется определенным интегралом 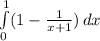 .
.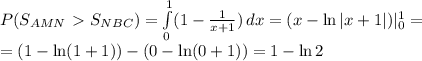
32 = 2 + 7 + 23
32 = 2 + 11 + 19
32 = 2 + 13 + 17