
ответ: 1680 кг
Пошаговое объяснение:
1/2 это половина от целой репки
1/2 * 1/3 = 1/6 от целой репки отдал бабке
1/2 - 1/6 = 3/6 - 1/6 = 2/6 = 1/3 от целой репки осталось после бабки
1/3 * 1/4 = 1/12 от целой репки отдал внучке
1/3 - 1/12 = 4/12 - 1/12 = 3/12 = 1/4 от целой репки осталась после внучки
1/4 * 1/5 = 1/20 от целой репки отдал жучке
1/4 - 1/20 = 5/20 - 1/20 = 4/20 = 1/5 от целой репки осталось после жучки
1/5 * 1/6 = 1/30 от целой репки отдал кошке
1/5 - 1/30 = 6/30 - 1/30 = 5/30 = 1/6 от целой репки осталось после кошки
1/6 * 1/7 = 1/42 от целой репки отдал мышке
1/6 - 1/42 = 7/42 - 1/42 = 6/42 = 1/7 от целой репки осталось после мышки
1/7 это 240 кг
240*7=1680 кг весила репка
Доказал ее великий Леонард Эйлер. Это формула
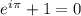
"е" в степени произведения "и" на "пи" плюс один равно 0
Здесь есть все важные области математики:
"пи" из геометрии
"и" из алгебры
"е" из математического анализа
единица из арифметики
2) Формула ГеронаФормула для вычисления площади треугольника со сторонами а, b и с
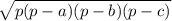 где
где 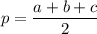 так называемый "полупериметр"
так называемый "полупериметр"
Корень из произведения полупериметра на разность полупериметра и первой стороны на разность полупериметра и второй стороны на разность полупериметра и третьей стороны
3) Формула КарданоМатематики очень долго пытались найти решение уравнений третьей степени, и Кардано смог найти такое
Решение уравнения 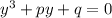
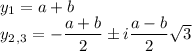
где
![a=\sqrt[3]{-\dfrac q2+Q}\\b=\sqrt[3]{-\dfrac q2-Q}](/tpl/images/1459/0100/f291b.png)
А Q в свою очередь равно
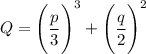
Корни многочлена 3 степени относительно х при старшем коэффициенте 1 и коэффициенте при х² 0 выражаются либо суммой а и б, или суммой или разности их полусуммы со знаком минус и их полуразности, умноженной на корень из минус трех, сами же эти числа равны кубическому корню из отрицательной половины свободного члена плюс или минус некоторое число Q, которое равно сумме куба трети коэффициента перед первой степенью и квадрата половины свободного члена
4) Бином НьютонаПростая формула для раскрытия скобок 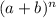 при натуральных n
при натуральных n
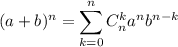
Сумма степеней а от n до 0 умноженные на степень b от 0 до n умноженные на число сочетаний из n по текущий член многочлена
5) Основная теорема арифметикиЛюбое натуральное число больше 1 можно разложить в произведение степеней простых чисел единственным образом с точностью до перестановки множителей
6) Основное Тригонометрическое Тождество (ОТТ)Эту формулу все знают со школы:
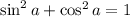
Сумма квадратов синуса и косинуса одного аргумента равна 1
7) Формула Эйлера для любого плоского графа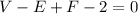
Число вершин в любом графе минус число ребер в этом же графе плюс число граней в этом же графе равно 2 для любого графа
8) Первый замечательный предел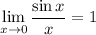
Отношение синуса к его аргументу при аргументе стремящимся к 0 равно 1 для любого аргумента
9) Второй замечательный предел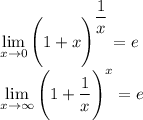
сумма 1 и х в степени обратной х при х стремящимся к 0 равно е
сумма 1 и обратной х в степени х при х стремящимся к бесконечности равно е
10) Разложение числа пи в ряд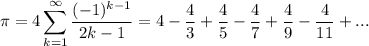
Пи равно учетверенной знакочередующейся сумме чисел обратных нечетным
Пошаговое объяснение:
1) НОД=4
36=2*2*3*3
40=2*2*2*5
2)НОД=1
17 - простое
24=2*2*2*3
3)НОД=16
16=2*2*2*2
32=2*2*2*2*2
4)НОД=5
15=3*5
40=2*2*2*5