 и
и 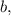 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
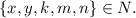
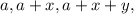 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и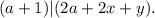
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;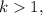 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.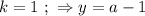 ;
;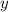 его значение
его значение 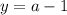 и будем искать такие комбинации
и будем искать такие комбинации 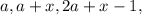 чтобы:
чтобы: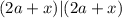 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 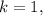
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и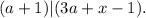
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;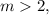 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.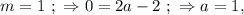 но это не подходит по условию.
но это не подходит по условию.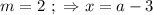 ;
; его значение
его значение 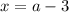 и будем искать такие комбинации
и будем искать такие комбинации 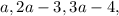 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 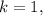
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 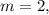
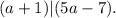
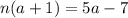 ;
;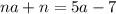 ;
; ;
;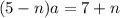 ;
;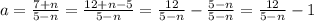 ;
;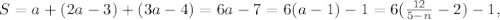
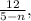 т.е. при
т.е. при 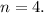
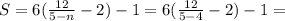
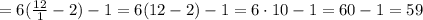 ;
;
Если сочетания "звание - специальность" не может быть, то соответствующую ячейку закрашиваем.
Рассматриваем первый тур. Так как каждый играл только один раз, то каждое сочетание "звание - специальность" из перечисленных в первом туре необходимо закрасить. По итогам первого тура никого из участников явно выделить не удалось.
Рассматриваем информацию про капитана. Так как он выбыл, то каждый из играющих в следующих турах не может быть капитаном. Также не может быть игроком отдыхающий в соответствующем туре, во втором туре - минометчик, в третьем туре - рядовой.
Рассматриваем второй тур. Аналогично первому туру, закрашиваем сочетания из перечисленных сведений, а также учитывая информацию про капитана и отдыхающего. Явные игроки не выявлены.
Рассматриваем третий тур. Аналогично первому и второму туру.
Явно определены следующие участники:
1) Лейтенант - связист
2) Прапорщик - минометчик
Вычеркиваем эти два столбца и две строки.
Определен следующий участник:
3) Сержант - десантник
Вычеркиваем соответствующий столбец и строку.
Следующий участник:
4) Полковник - ракетчик
Вычеркиваем соответствующий столбец и строку.
Следующие участники:
5) Майор - артиллерист
6) Капитан - летчик
Остается набор "ефрейтор", "рядовой", "пехотинец", "танкист". Обращаем внимание, что рядовой не участвовал в третьем туре, а танкист - в шестом (это условие можно было отметить в таблице на предыдущих шагах). Значит, рядовой - не танкист, тогда последние участники:
7) Рядовой - пехотинец
8) Ефрейтор - танкист