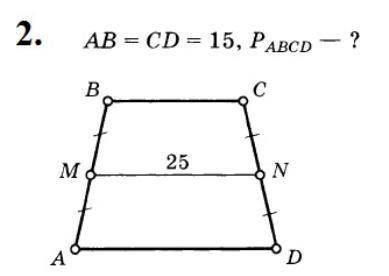
Математика: Нужно найти периметр трапеции с решением

Нужно найти периметр трапеции
с решением

Нужно найти периметр трапеции с решением

👇

Увидеть ответ

Открыть все ответы

Ответ:

angel020580

03.07.2022

36-x=20
x=36-20
x=16
ответ:16
Чтобы решить линейное уравнение, нужно с допустимых преобразований оставить неизвестную величину в одной стороне от знака равенства, а известные величины отправить в другую сторону.
Сделать это можно с прибавления одного и того же числа к обеим частям уравнения, вычитания одного и того же числа из обеих частей уравнения, умножения и\или деления обеих частей уравнения на одно и то же число, неравное нулю.
36-x=20
x=36-20
x=16
ответ:16

82-d=5
x=82-5
x=77
ответ:77

x-64=9
x=64+9
x=73
ответ:73

4,6(38 оценок)

Ответ:

Nikita43242

03.07.2022

ответ: $\begin{array}{|c|c|c|c|c|}R & r & a_n & P & S\\3\sqrt{2} & 3 & 6 & 24 & 36\\2\sqrt{2} & 2 & 4 & 16 & 16\\4 & 2\sqrt{2} & 4\sqrt{2} & 16\sqrt{2} & 32\\7\sqrt{2} & 3,5 & 7 & 28 & 49\\2\sqrt{2} & 2 & 4 & 16 & 16\\\end{array}$

Пошаговое объяснение:

Заданы формулы для правильного многоугольника.

В нашем случае правильного четырехугольника или квадрата.

Заданы формулы:

Длина многоугольника через радиус описанной окружности

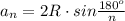
$a_n=2R \cdot sin\frac{180^o}{n}$

Для квадрата

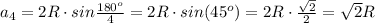
$a_4=2R \cdot sin\frac{180^o}{4}=2R \cdot sin(45^o)=2R\cdot\frac{\sqrt{2}}{2}=\sqrt{2}R$

или

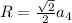
$R=\frac{\sqrt{2}}{2}a_4$

Радиус вписанной окружности через радиус описанной окружности

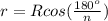
$r=Rcos(\frac{180^o}{n})$

Для квадрата

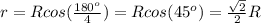
$r=Rcos(\frac{180^o}{4})=Rcos(45^o)=\frac{\sqrt{2}}{2}R$

или

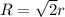
$R=\sqrt{2}r$

Площадь многоугольника через периметр и радиус вписанной окружности

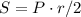$S=P\cdot r/2$ или S =a_4^2

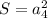
Определим значения первой строки таблицы зная, что сторона квадрата a = 6.

Радиус описанной окружности

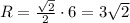
$R=\frac{\sqrt{2}}{2}\cdot 6=3\sqrt{2}$

Радиус вписанной окружности

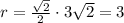
$r=\frac{\sqrt{2}}{2}\cdot3\sqrt{2}=3$

Периметр

$P= 4a_4=4\cdot6=24$

Площадь квадрата

$S=24\cdot 3/2 = 36$

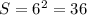
или S= 6^2=36

Определим значения второй строки таблицы зная, что радиус вписанной окружности r=2.

Радиус описанной окружности

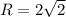
$R=2\sqrt{2}$

Длина стороны квадрата

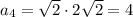
$a_4=\sqrt{2}\cdot2\sqrt{2}=4$

или

$a_4=2r=2\cdot2=4$

Периметр

$P= 4a_4=4\cdot4=16$

Площадь квадрата

$S=16\cdot 2/2 = 16$

Определим значения третьей строки таблицы зная, что радиус описанyой окружности R=4.

Длина стороны квадрата

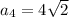
$a_4=4\sqrt{2}$

Радиус вписанной окружности

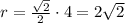
$r=\frac{\sqrt{2}}{2}\cdot4=2\sqrt{2}$

Периметр

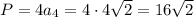
$P= 4a_4=4\cdot4\sqrt{2}=16\sqrt{2}$

Площадь квадрата

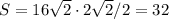
$S=16\sqrt{2}\cdot 2\sqrt{2}/2 = 32$

Определим значения четвертой строки таблицы зная, что периметр квадрата P=28.

Длина стороны квадрата

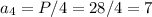
a_4=P/4 =28/4=7

Радиус описанной окружности

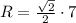
$R=\frac{\sqrt{2}}{2}\cdot 7$

Радиус вписанной окружности

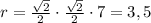
$r=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{2}}{2}\cdot 7=3,5$

Площадь квадрата

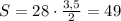
$S=28\cdot \frac{3,5}{2} = 49$

Определим значения пятой строки таблицы зная, что площадь квадрата S=16.

Длина стороны квадрата

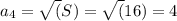
$a_4=\sqrt(S) =\sqrt(16)=4$

Далее как для второй строки.

Повторять не буду

Подставим значения в таблицу

$\begin{array}{|c|c|c|c|c|}R & r & a_n & P & S\\3\sqrt{2} & 3 & 6 & 24 & 36\\2\sqrt{2} & 2 & 4 & 16 & 16\\4 & 2\sqrt{2} & 4\sqrt{2} & 16\sqrt{2} & 32\\7\sqrt{2} & 3,5 & 7 & 28 & 49\\2\sqrt{2} & 2 & 4 & 16 & 16\\\end{array}$

4,8(9 оценок)

Это интересно:

Хобби-и-рукоделие

24.01.2022

Как сделать клей Mod Podge: простые инструкции...

Компьютеры-и-электроника

10.03.2020

Как быстро и просто повернуть экран компьютера?...

Здоровье

04.12.2021

Как предотвратить появление прыщей: советы от специалистов...

Семейная-жизнь