Найди значение выраза 0,129: a + b : 100, если а=64,5,b = 2,9. ответ округлите до сотых

👇

Увидеть ответ

Ответ:

апрркн1

12.01.2023

1. 0,129/64,5=0,002

2. 2,9/100=0,029

3. 0,002+0,029=0,031 и округляем до сотых 0,03

4,6(45 оценок)

Открыть все ответы

Ответ:

Pr0100Chell

12.01.2023

Пошаговое объяснение:

1) Определим значения выражения 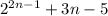$2^{2n-1}+3n-5$ при различных значениях 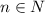$n \in{N}$ как последовательность

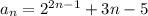
$a_{n}=2^{2n-1}+3n-5$

2) Определим значения членов 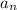a_n последовательности при n=1, n=2, n = 3:

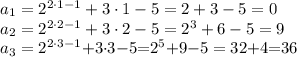
$a_1=2^{2\cdot1-1}+3\cdot1-5 = {2} + 3 - 5 = 0 \\ a_2=2^{2\cdot2-1}+3\cdot2-5 = {2}^{3} + 6 - 5 = 9 \\ a_3=2^{2\cdot3-1}{+}3{\cdot}3{-}5{=}{2}^{5} { +}9 {-} 5 =32{ +} 4{ =}36 \\$

3) Применим метод математической индукции.

3a) Возьмем такой член 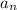a_n , который кратен 9 (как мы убедились выше, такое 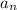a_n существует (например, а3))

Т.к. он кратен 9, обозначим его как

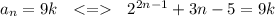
$a_n=9k \:\:\: \:\:\:2^{2n-1}+3n-5=9k$

3b) Вычислим значение 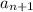$a_{n+1}$ ,

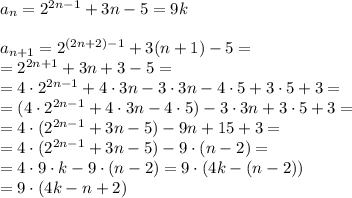
$a_{n} = 2^{2n-1}+3n-5 = 9k \\ \\ a_{n + 1} = 2^{(2n + 2)-1}+3(n + 1)-5 = \\ = 2^{2n + 1}+3n + 3-5 = \\ =4 \cdot2^{2n - 1}+4 \cdot3n - 3 \cdot3n-4 \cdot5 +3 \cdot5 + 3 = \\ =(4 \cdot2^{2n - 1}+4 \cdot3n -4 \cdot5) - 3 \cdot3n+3 \cdot5 + 3 = \\ = 4 \cdot(2^{2n - 1} + 3n - 5) - 9n + 15 + 3 = \\ = 4 \cdot(2^{2n - 1} + 3n - 5) - 9\cdot( n - 2) = \\ = 4 \cdot9\cdot{k} - 9 \cdot(n - 2) = 9 \cdot(4{k} - (n - 2)) \\ = 9 \cdot(4{k} - n + 2)$

Как мы видим, мы получили, что 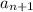$a_{n+1}$ равно произведению, один из множителей которого равен 9, а следовательно, 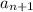$a_{n+1}$ также кратен 9 Следовательно кратность 9 справедлива и для последующих значений последовательности.

Что и требовалось доказать

4,6(98 оценок)

Ответ:

Onewood

12.01.2023

Насколько я понимаю, мы имеем:

х( -/+) у, тоесть нам нужно сделать определенные действия ( вычесть либо суммировать) с х и у.

Далее мы видим 2х+у, х<у; 3у, х=у; х²-5у, х>у. Это значит, что если х меньше у, наше задание равно 2х+у, если х и у равны, уравнение - 3у, если х больше у, уравнение - х²-5у

У нас есть:

(1 ? 2) ? (3 ? 1).

Нам необходимо понять, какое это из тех трёх уравнений.

Это не может быть х²-5у, так как у нас нету ни квадрата, ни 5.

Остаётся 2х+у и 3у.

Если ответ - 2х+у, значит х<у.

Пусть х=1, у=3. Условие х<у выполняется, подставим эти значения в уравнение 2х+у

2×1+3×1 = 5. На этом я ожидал окончания решения, но, увы, не всё так просто. Значит, продолжим.

(1 ? 2) ? (3 ? 1)

В скобках не может быть умножение или деление, так как в таком случае при любом действии между скобок мы не получим ни 10, ни 11, 12 и т.д.

Соответственно, в скобках либо + либо -.

В первой скобке не может быть -, так как тогда значение уравнения будет <5.