ответ:
распределительное. распределительное свойство применяется только относительно сложения. распределительное свойство гласит: если число умножается на сумму, то можно каждое из слагаемых умножить на это число, а результаты сложить.
сочетательное.
сочетательное свойство говорит о том, что при перемножении трех и более чисел, можно перемножить два первых числа, а результат использовать дальше в качестве множителя. то есть 3*4*5=12*5=60
переместительное. переместительное свойство гласит, от перемены мест множителей произведение не меняется.
распределительное свойство может применяться и относительно вычитания или деления. с этого свойства раскрывают скобки в примерах при необходимости.
переместительное свойство
правильное использование определения переместительного свойства умножения может увеличить скорость счета. к сожалению, специальных правил группировки нет. нужно полагаться только на собственный опыт и логику. рассмотрим небольшой пример, чтобы показать применение свойства на практике:
((15*25*7*3: 125)-3): 12 – в этом примере можно только правильно сгруппировав произведение в скобках для ускорения деления. для этого представим число 15 в виде произведения 3*5
((15*25*7*3: 125)-3): 12=((5*3*25*7*3: 125)-3): 12 теперь перемножим 5 и 25, выполним деление произведения на число. для этого можно только один из множителей разделить на это число, а потом результат использовать, как один из множителей.
*25)*3*7*3: 125)-3): 12=((125*3*7*3: 125)-3): 12=(3*3*7-3): 12=(9*7-3): 12=(63-3): 12=60: 12=5
без переместительного свойства не удалось бы правильно сгруппировать множители, а значит пришлось бы считать пример полностью, что отняло бы большое количество времени
Пошаговое объяснение:
1) pi/4+2pi*n<= x<= 7/4pi+2pi*n, где n принадлежит Z
2)-3pi/4+2pi*n<= x<= 3/4pi+2pi*n, где n принадлежит Z
3) -pi/6+2pi*n<= x<= 7/6pi+2pi*n, где n принадлежит Z
4) pi/6+2pi*n<= x<= 5/6pi+2pi*n, где n принадлежит Z
5) -pi/4+2pi*n<= x<= pi/4+2pi*n, где n принадлежит Z
6) -pi/6+2pi*n<= x<= pi/6+2pi*n, где n принадлежит Z
7) -5/6pi+2pi*n<= x<= 5/6pi+2pi*n, где n принадлежит Z
8) -7/6pi+2pi*n<= x<= pi/6+2pi*n, где n принадлежит Z
9) -5/6pi+2pi*n<= x<= -pi/6+2pi*n, где n принадлежит Z
10) 2pi*n, т.к. область значений cos и sin [-1;1]
11) (-беск;+беск)
12) pi/3+2pi*n<= x<= 2/3pi+2pi*n, где n принадлежит Z
13)-3pi/4+2pi*n<= x<= 3/4pi+2pi*n, где n принадлежит Z
Я Вам все не могу объяснить,много писать,но если хотите разобраться, то вот сайт https://egemaximum.ru/prostejshie-trigonometricheskie-neravenstva/
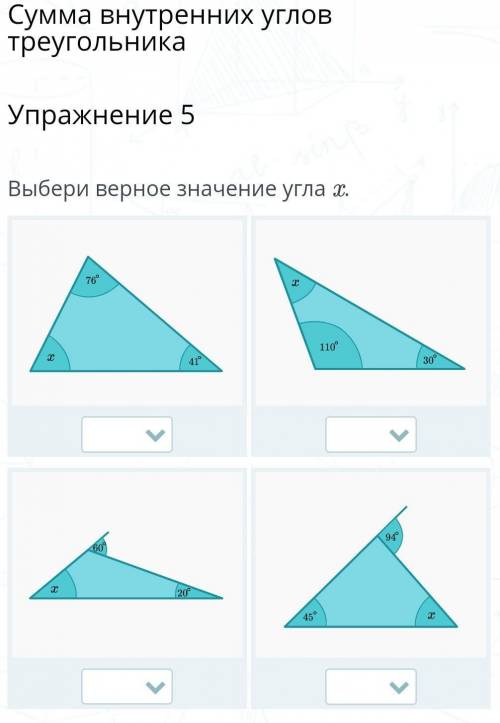
1 - 63 градуса 2(где 110)-40 градусов 3-60 градусов 4-41 градус