15330.
Пошаговое объяснение:
1) Наименьшим трёхзначным числом, кратным трём, является число 102. Каждое следующее на 3 больше предыдущего. По определению все они образуют арифметическую прогрессию (аn), в которой а1 = 102, d = 3, an < 320.
2) аn = a1 + d(n - 1) = 102 + 3(n - 1) = 102 + 3n - 3 = 99 + 3n.
По условию an < 320, тогда
99 + 3n < 320
3n < 320 - 99
3n < 221
n < 73 2/3
В последовательности 73 члена.
3) S73 = (2a1 + 72d)/2 • 73 = (a1 + 36d) • 73 = (102+36•3) • 73 = (102+108) • 73 = 210 • 73 = 14600 + 730 = 15330.
Пусть во второй шеренге
гномов, тогда в первой 
.
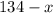Тогда промежутков между гномами второй шеренги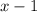
штук.
А число гномов из первой шеренги можно представить как число гномов второй и плюс еще число промежутков, умноженное на 2, то есть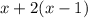
. При этом данное число совпадает с 
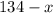. Составим уравнение:
То есть гномов во второй шеренге 34, а в первой 134 - 34 = 100.
Задачу можно было решить и таким уравнением:
В любом случае, получается тоже самое.