
График в приложении.
По оси OX отложим время, начиная с 10 часов, так как движение началось в 10 часов утра. Единичный отрезок = 1 часу.
По оси OY отложим расстояние в км начиная от 0 (от точки выезда), с единичным отрезком равным 20 км (для удобства).
Проводим отрезки в соответствии с условием задачи:
Скорость до остановки была 50 км/ч, время в пути 2 часа (каждый час по 50 км).
Остановка 30 мин = 1/2 часа, скорость = 0.
Скорость после остановки 60 км/ч, время в пути 1 час (проехал 60 км за 1 час).
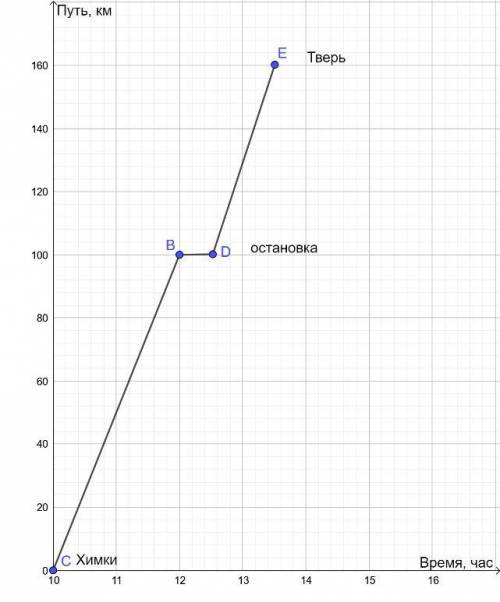
По графику:
1) Расстояние от Химок до Твери 160 км.
2) В Тверь автобус прибыл в 13,5 часов = 13 часов 30 минут.
3) В 12 часов дня автобус был на расстоянии 100 км от Химок и 60 км от Твери.
минимум 6 пар.
Пошаговое объяснение:
Назовём каждую батарейку отдельной буквой — А Б В Г Д Е Ж З И К Л М Н. Это позволит нам не перепутать батарейки, когда мы будем менять их местами друг с другом.
Теперь разобьём батарейки на пары и проверим в фонарике каждую из них: (А Б) (В Г) (Д Е) (Ж З) (ИК) (ЛМ) (Н)
Если фонарик заработал на какой-то из них — отлично, мы нашли нужную пару.
Если лампочка так и не загорелась, значит, в каждой паре у нас оказалась одна хорошая батарейка, и одна плохая.
Теперь возьмём любые две пары — например, (А Б) и (В Г) — и поменяем в них первые батарейки местами.
(В Б) и (А Г) — в этот момент мы проверили уже шесть пар.
Получим: Если фонарик не заработал и после этой перестановки, значит, мы поменяли местами одинаковые батарейки: хорошую заменили на хорошую, или плохую — на плохую. Выходит, нужно взять вторую батарейку из первой пары и поменять её с первой батарейкой из второй пары: берём пару (В Б), достаём оттуда вторую батарейку Б и ставим её на первое место в паре (А Г), получаем: (Б Г) — это седьмая пара.
Если фонарик загорелся, значит, второй мы поставили хорошую батарейку. Если фонарик всё ещё не светит, получается, в этой паре у нас две плохих батарейки, а две хороших остались в другой — (В А). Ставим их в фонарик, и готово!
Получается, что нам понадобится проверить минимум 6 пар.