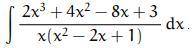
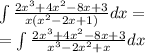
разделим числитель на знаменатель:
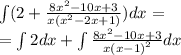
второй интеграл решаем с неопределенных коэффициентов:
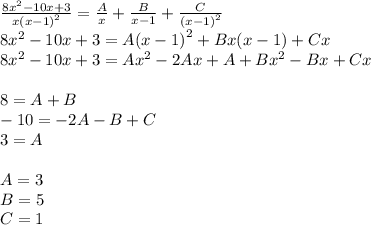
получаем:
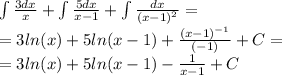
прибавляем решение первого интеграла, ответ:
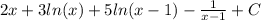
У меня калькулятор не выдерживает таких больших чисел, так что только выражения могу предложить.
Основные формулы которые мы используем:
Вероятность P=M/N, где М - количество благоприятных исходов, N - все возможные исходы.
Комбинация Cₙˣ=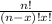 , где из множества n мы берем x элементов
, где из множества n мы берем x элементов
N=С₁₇₂¹⁶ - столькими можно выбрать цветы в один день
M=С₁₆₆¹⁵*С₆¹+С₁₆₆¹⁴*С₆²+С₁₆₆¹³*С₆³+С₁₆₆¹²*С₆⁴+С₁₆₆¹¹*С₆⁵+С₁₆₆¹⁰*С₆⁶ - столько вариантов благоприятных исходов (хоть один новый цветок в день).
Р=(С₁₆₆¹⁵*С₆¹+С₁₆₆¹⁴*С₆²+С₁₆₆¹³*С₆³+С₁₆₆¹²*С₆⁴+С₁₆₆¹¹*С₆⁵+С₁₆₆¹⁰*С₆⁶)/С₁₇₂¹⁶
Должно получиться число меньше 1
ответ:3ln(x)+5ln(x-1) - 1/(x-1) +2x+C
Пошаговое объяснение: Выполним деление числителя на знаменатель столбиком, тогда J= ∫((8x²-10x+3)/x·(x²-2x+1) + 2)dx= ∫ (8x²-10x+3)dx/x·(x²-2x+1) + 2∫dx=∫ (8x²-10x+3)dx/x·(x-1)² + 2∫dx
Вычислим сначала первое слагаемое J₁=∫ (8x²-10x+3)dx/x·(x-1)² =
∫(3/x+ 5/(x-1) + 1/(x-1)²)dx=3∫dx/x+ 5∫dx/(x-1) + ∫dx(x-1)² =
3ln(x)+5ln(x-1) - 1/(x-1) +C ⇒ Весь интеграл: J=J₁ +2∫dx=3ln(x)+5ln(x-1) - 1/(x-1) +2x+C