х max = -1/3; x min = 0
Пошаговое объяснение:
Исследовать функцию на экстремумы и нарисовать её график.

Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.
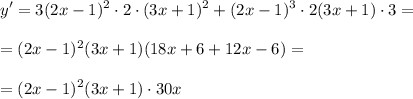
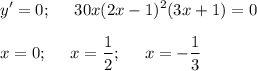
См. вложение.
Если "+" - функция возрастает, если "-" - функция убывает.Функция возрастает на промежутках: (-∞; -1/3]; [0; +∞).
Убывает на промежутках: [-1/3; 0]
Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.х max = -1/3; x min = 0
y(-1/3) = 0; y(0) = -1
Обозначим эти точки на координатной плоскости и нарисуем график.

y=(2x-1):2(х-2) [-1;2]
y '=2≠0
y(-1)=-3:-6=0,5
y(2)=3:4= ¾
ответ: y (min)=¾ , y (max)=0,5
Второе мне сложное, боюсь не правильно решить