№1 х=3, у=4 или х=4, у=3
х²+у²=25
х+у=7
х=7-у, подставляем данное выражение в первое уравнение и решаем
(7-у)²+у²=25
49-14у+у²+у²=25
2у²-14у+24=0
у²-7у+12=0
Находим дискриминант
D=7²-4·1·12=49-48=1, значит будет два корня
 =(7-
=(7- )/2=6/2=3
)/2=6/2=3
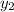 =(7+
=(7+ )/2=8/2=4
)/2=8/2=4
теперь находим значения х
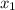 =7-у=7-3=4
=7-у=7-3=4
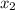 =7-у=7-4=3
=7-у=7-4=3
№2 х=1, у=2
3х²+у²=7
х²+2у²=9
домножаем каждый член первого уравнения на (-2)
-6х²-2у²=-14
х²+2у²=9
складываем почленно левую и прав. части уравнений системы уравнений
-5х²=-5
5х²=5
х²=1
х= =1 теперь находим у
=1 теперь находим у
у²=7-3х²=7-3=4
у= =2
=2
№3 х=2, у=3
2х-у=1
3х+2у=12
домножаем каждый член первого уравнения на 2
4х-2у=2
3х+2у=12
складываем почленно левую и прав. части уравнений системы уравнений
7х=14
х=14÷7=2
находим значение у
у=2х-1=4-1=3
№4 длина 6 см, ширина 3 см
пусть а см - длина прямоугольника, b см - ширина
составляем систему уравнений
а²+b²=45
(а+b)·2=18
упрощаем
а²+b²=45
а+b=9 то есть b=9-а и подставляем в первое уравнение
а²+(9-а)²=45 и решаем
а²+81-18а+а²=45
2а²-18а+36=0 сокращаем на 2
а²-9а+18=0
находим дискриминант
D=81-4·18=81-72=9
теперь находим по формуле корней длину прямоугольника
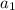 =(9+
=(9+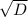 )/2=(9+3)/2=6
)/2=(9+3)/2=6
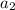 =(9-
=(9-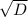 )/2=6/2=3
)/2=6/2=3
находим ширину прямоугольника
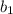 =9-a=9-6=3
=9-a=9-6=3
 =9-3=6
=9-3=6
по смыслу подходит длина 6 см, тогда ширина 3 см
№5 длина 12 см, ширина 5
пусть а см - длина прямоугольника, b см - ширина
так как диагональ - это гипотенуза в треугольнике, где катеты это стороны прямоугольника
составляем систему уравнений
(а+b)·2=34
a²+b²=13²
то есть
а+b=17
a²+b²=169
выражаем b=17-a и подставляем во второе уравнение
а²+(17-а)²=169 и решаем
а²+289-34а+а²=169
2а²-34а+120=0 сокращаем на 2
а²-17а+60=0
находим дискриминант
D=17²-4·60=289-240=49 D больше 0, значит два корня
теперь находим по формуле корней длину прямоугольника
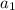 =(17-
=(17-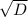 )/2=(17-7)/2=5
)/2=(17-7)/2=5
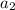 =(17+
=(17+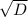 )/2=(17+7)/2=12
)/2=(17+7)/2=12
теперь находим ширину
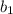 =17-a=17-5=12
=17-a=17-5=12
 =17-a=17-12=5
=17-a=17-12=5
по смыслу подходит 12 см - длина, тогда 5 см - ширина
Пошаговое объяснение:
всё есть здесь
Пошаговое объяснение:
Теория:
Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»
Aksiala9.jpg
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
111.jpg
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны относительно некоторой точки O, если точка O является серединой отрезка MM1.
Simetrija_c_punkti.png
Точка O называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.
Simetrija_c.png
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно центра (точки) O:
1. для этого соединим точки A, B, C с центром O и продолжим эти отрезки;
2. измерим отрезки AO, BO, CO и отложим с другой стороны от точки O равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Simetrija_ass_punkti.png
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Simetrija_ass.png
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно красной прямой:
1. для этого проведём из вершин треугольника ABC прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
Для равнобедренного треугольника есть единственная ось симметрии.
Для равностороннего треугольника — три оси.
Для прямоугольника и ромба существуют две оси симметрии.
Для квадрата — целых четыре.
Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
1) идёт уменьшение через 20
2) идёт увеличение сначала через 10 потом через 20
дальше не чего не понятно ну вот 2 есть