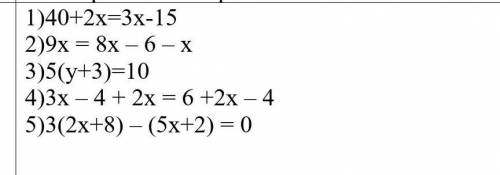
1)2х-3х=-15-40
-1х=-55
х=-55:(-1)
х=55
2)9х-8х+х=6
2х=6
х=6:2
х=3
3)5у+15=10
5у=10-15
5у=-5
у=-5:5
у=-1
4)3х+2х-2х=6-4+4
3х=6
х=6:3
х=2
5)6х+24-5х-2=0
6х-5х=-24+2
х=-22
0
Пошаговое объяснение:
См. пошаговое объяснение
Пошаговое объяснение:
1) Опустим перпендикуляр из вершины основания 8 см на основание 14 см. Получим две фигуры:
- прямоугольник, у которого две противоположные стороны равны 8 см, а две другие противоположные стороны также равны между собой, но нам их длина не известна;
- прямоугольный треугольник, у которого высота (1-й катет) - это та самая сторона прямоугольника, которая нам не известна, и второй катет, длина которого равна: 14 - 8 = 6 см; а гипотенуза - это боковая сторона трапеции (которую надо найти).
2) В получившемся прямоугольном треугольнике один угол равен 90 градусам (по построению), а другой угол равен 60 градусам, согласно условию. Следовательно, 3-й угол этого треугольника равен:
180 - 90 - 60 = 30 градусов.
3) В условии не сказано, какой именно из углов равен 60 градусам: тот, которой примыкает к верхнему основанию длиной 8 см, или угол, сторона которого является частью большего основания.
Поэтому рассмотрим оба варианта решения.
4) Вариант 1: второй катет лежит против угла в 30 градусов.
Катет, лежащий против угла в 30 градусов, равен половине гипотенузы; значит, гипотенуза (она же - боковая сторона трапеции) в два раза длиннее:
6* 2 = 12 см - это первый вариант ответа.
5) Вариант 2: второй катет лежит против угла в 60 градусов.
Катет равен гипотенузе, умноженной на синус угла, противолежащего этому катету.
Синус угла 60 градусов = √ 3/2.
Пусть х - длина гипотенузы, тогда:
6 = х * (√ 3/2), откуда х = 6 : (√ 3/2) = 12/√ 3, что примерно равно
12 : 1,732 = 6,93 см.
1) 40+2x=3x-15
2x-3x=-15-40
-1x=-55 /(-1)
x=55
2) 9x=8x-6-x
9x-8x+x=-6
2x=-6 /2
x=-3
3) 5(y+3)=10
5y+15=10
5y=10-15
5y=-5 /5
y=-1
4) 3x-4+2x=6+2x-4
3x+2x-2x=6-4+4
3x=6 /3
x=2
5) 3(2x+8)-(5x+2)=0
6x+24-5x-2=0
6x-5x=-24+2
x=-22