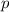 и
и 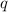
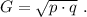
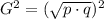
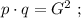
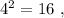 а произведение двух самых больших равно
а произведение двух самых больших равно 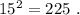 »
»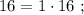
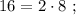
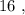 т.е.:
т.е.: 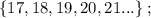
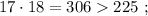
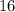 каждое – будет, очевидно, больше чем
каждое – будет, очевидно, больше чем 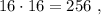 т.е. больше
т.е. больше 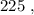 а значит, при выборе минимальных чисел в виде
а значит, при выборе минимальных чисел в виде  и
и 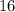 – подобрать остальные числа невозможно.
– подобрать остальные числа невозможно.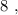 т.е.:
т.е.: 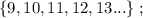

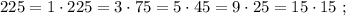
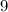 и
и 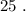
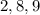 и
и 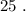
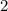 и
и 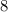 Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 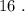
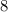 и
и 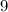 никаких натуральных чисел нет.
никаких натуральных чисел нет.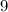 и
и 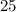 Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 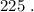
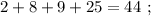

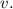 Тогда скорость Феди равна
Тогда скорость Феди равна 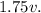 Когда Федя догоняет Женю, их скорость сближения равна
Когда Федя догоняет Женю, их скорость сближения равна 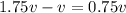 (вычитаем, поскольку Женя уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Иначе можно сказать, что скорость Жени в
(вычитаем, поскольку Женя уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Иначе можно сказать, что скорость Жени в 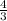 раза больше, чем скорость сближения, поскольку
раза больше, чем скорость сближения, поскольку 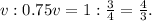
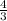 раза большее расстояние, поскольку её скорость в
раза большее расстояние, поскольку её скорость в 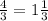 раза больше скорости сближения.
раза больше скорости сближения.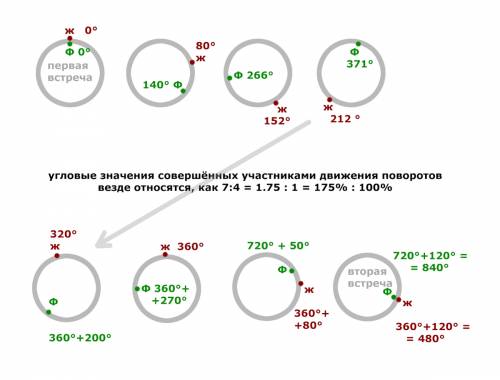
)56.7-12.5+9-27.5+13.3=39
2а)8-6к
б)4с-4-7с-35-6с-16=-9с+23
30.9б-4.5-0.8б+1.6=2.3
30.1б=5.2
б=0.1727575(можно дробью написать)