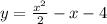
Выполним построение опираясь на геометрический смысл производной и не только. Для начала найдём все пересечения с осями координат.
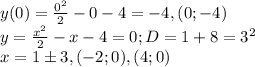
Выделим полный квадрат.
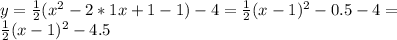
Из этого следует, что для (x-1) функция чётная, то есть имеет вертикальную ось симметрию, поэтому для нашей функций x=1 это вертикальная ось симметрии.
Теперь найдём первую производную.
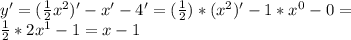
Если x>1, то производная положительная, значит функция возрастает.
Если x<1, то производная отрицательная, значит функция убывает.
При х=1, производная равна нулю и меняет свой знак с минуса на плюс, поэтому это минимум функции.
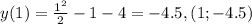
Теперь найдём вторую производную.
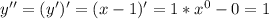
Как видно производная всегда всегда положительная, поэтому функция всегда выпукла вниз.
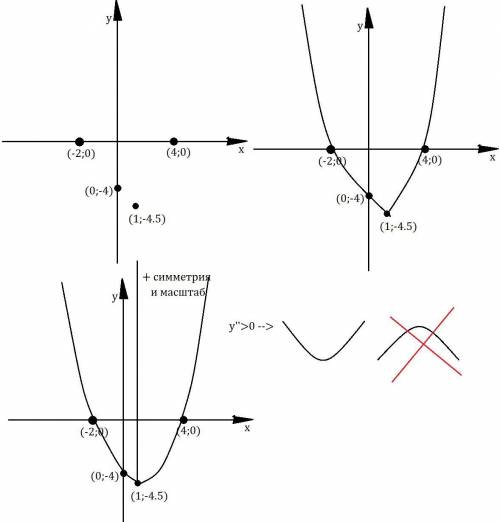
Смотри построение внизу.
f(x) = tg²(x)
f'(x) = 2 tg(x) * (tg(x))' = 2 sin(x) ÷ cos³(x)
Далее, методом интервалов.
Ищем корни f'(x) = 0
sin(x) = 0
Корни: x = πk, k - целое
Осталось определить знаки. В первой четверти и синус, и косинус положительны. В третьей четверти и синус, и косинус отрицательны.Значит в точках из промежутка [ 0+πk ; π/2 + πk ] функция возрастает. Иначе убывает.