Существует
Пошаговое объяснение:
На самом деле такое число найдётся для любой натуральной степени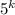 
.
Я утверждаю, что для всех k найдётся число, состоящее из k цифр, не содержащее нулей в десятичной записи и делящееся на .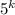
Доказываем по индукции.
База индукции. Для k = 1 подходит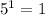 
.
Индукционный переход. Пусть длина числа 
равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на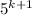 
.
Получившееся число равно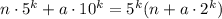 
, оно будет делиться на 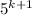, если делится на 5.
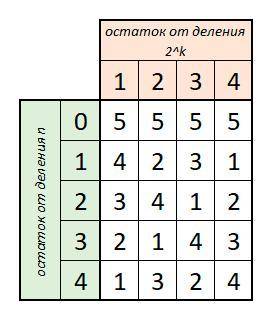
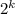при делении на 5 может давать остатки 1, 2, 3 и 4; n может давать любые остатки от 0 до 4. Ниже в таблице я явно выписываю, какие можно взять a для каждой комбинации остатков. Например, если n даёт остаток 3 при делении на 5; 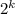даёт остаток 4 при делении на 2, то можно взять a = 3: тогда 
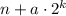даёт такой же остаток при делении на 5, что и 
.
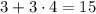Таким образом, если для k такое число найдётся, то и для k + 1, а значит, и для всех k, в том числе и для k = 1987.
Вот, например, числа, построенные для k от 1 до 20:
5 25 125 3125 53125 453125 4453125 14453125 314453125 2314453125 22314453125 122314453125 4122314453125 44122314453125 444122314453125 4444122314453125 54444122314453125 254444122314453125 1254444122314453125 21254444122314453125Например, число 21254444122314453125 делится на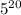 
и не содержит нулей :)
легкая атлетика» доклад по физкультуре что такое легка атлетика? легкая атлетика является олимпийским видом спорта, в него включены спортивная ходьба, беговые виды, пробеги, многоборья, технические виды и кроссы. ее по праву называют королевой спорта, так как она считается самым массовым видом спорта, а по количеству медалей в ее дисциплинах разыгрывалось всегда наибольшее количество медалей. в 1912 году была основана международная ассоциация легкоатлетических федераций со штаб квартирой в монако. легкая атлетика: развития
легкая атлетика – это древний вид спорта, о чем говорят численные археологические находки. самым ранним легкоатлетическим видом является бег. зародился этот вид спорта в древней греции. греки, кстати, все называли атлетикой, деля ее на «тяжелую» и «легкую». к тяжелой атлетике они относили , которые развивали сила, а к легкой те, которые развивали выносливость и ловкость. первый олимпийский легкоатлетический чемпион – короибос, получивший данный титул в 776 году до н.э. кстати, этот год и считается датой рождения легкой атлетики. современная этого вида спорта начала свое исчисление с 1837 года, когда произошли соревнования в беге на 2-вух километровой дистанции в городе регби. позже в его программу включили бег на короткие дистанции, метание тяжести, бег с препятствиями, прыжки в высоту и длину с разбега. с целью популяризации легкой атлетики в 1865 году основали лондонский атлетический клуб, а в 1865 году – любительскую атлетическую ассоциацию. бурное ее развитие связано с олимпийскими играми 1896 года, когда ей отвели наибольшее место.
правила: победителем считается команда или спортсмен, показавшие самые лучшие результате в финальных технических дисциплинах или финальных забегах. количество участников определяется регламентом соревнования, причем женщины и мужчины участвуют в разных стартах. стадионы бывают открытого и закрытого типа, часто совмещен с футбольным полем. открытый стадион состоит из секторов для технических дисциплин и 400 м дорожки, поделенной на 9 дорожек. закрытый стадион состоит из 200 м дорожки с 4-6 секторами. виды легкой атлетики спортивная ходьба. ноги спортсмена постоянно контактируют с землей. дистанции бывают 10 000 м, 20 000 м, 30 000 м и 50 000 м. бег. он представлен такими — бег на длинные дистанции, бег на средние дистанции, спринт, эстафета и барьерный бег. прыжки. делятся на горизонтальные (тройной прыжок, прыжок в длину) и вертикальные (прыжки с шестом, прыжки в высоту). метания. спортсмены перемещают снаряд на максимальное расстояние от себя. виды — толчок ядра, бросок мяча или гранаты, метание диска, молота или копья. многоборья. включает в себя соревнования одного вида дисциплины или нескольких видов спорта.