ответ:4
Пошаговое объяснение: начиная от 5!, все факториалы делятся без остатка на 5 (и на 10). Поэтому выражение в скобках можно записать как 1!+2!+3!+4!+10*а, где а-натуральное число. Сумма первых четырёх факториалов это 1+2+6+24=33=3+10*3. Т.е. выражение в скобках принимает форму 10*b+3, где b- натуральное число (выражение в скобках даёт остаток 3 при делении на 5). Если ты возведёшь это в квадрат, то получишь 100b^2+60b+9. Первые два делятся без остатка на 5, а третий даёт остаток в 4. Т.о., остаток равен четырём.
Гг
Пошаговое объяснение:
1) i ^ 13 = (i^2)^6 * i = (-1)^6 * i = i
i^100 = (i^2)^50 = (-1)^50 = 1
i^1993 = (i^100)^19 * i^93 = 1 * (i^2)^46 * i = i
2) (1 + i)^10
Воспользуемся формулой Муавра
z^n = r^n(cos φn + i*sin φn)
r - модуль, φ - аргумент комплексного числа
В нашем случае r = √2, φ = 
/4
(1 + i)^10 = (√2)^10 * (cos 10/4 + i*sin 10/4) = 32*(cos 5/2 + i*sin 5/2)=
= 32*(0+i*1) = 32i
Другой вариант решения:
(1 + i)^10 = ( (1 + i)^2 )^5 = (1 - 2i + i^2)^5 = (1 + 2i - 1)^5 = (2i)^5 = 32i * i^4 = 32i
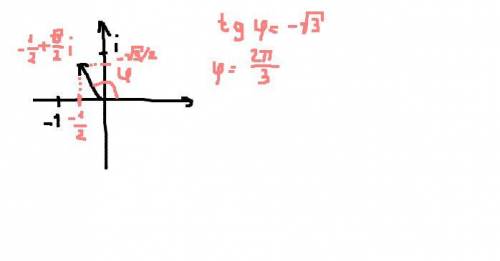
3) a = -1/2 + √3/2 * i
z^n = r^n(cos φn + i*sin φn)
Посчитаем модуль комплексного числа a:
r =√( (-1/2)^2 + (√3/2)^2) = 1
Аргумент φ = 2/3
a^4 = 1^4 * (cos 8/3 + i*sin 8/3) = -1/2 + i*√3/2 = a
a^11 = 1^11 * (cos 22/3 + i*sin 22/3) = -1/2 - i*√3/2
a^1992 = (a^4)^498 = a^498 =
= 1^498 * (cos 498*2/3 + i*sin 498*2/3) = cos 332 + i*sin 332 =
= 1
4) ( (1 + i)/(1 - i) )^1998 = ( (1 + i)^2 / 1^2 - i^2 )^1998 = ((1 + i)^2 / 2)^1998 =
= ((1^2 + 2i + i^2)/2)^1998 = ((1 +2i - 1)/2)^1998 = i^1998 = (i^2)^999 =
= (-1)^999 = -1
Пошаговое объяснение:
а) (BMK) ∩ (ADD1) = KM,
(BCC1) || (ADD1), следовательно,
(BMK) ∩ (BCC1) = BT || KM. Проведём AM1 || KM.
DM = 4/5 DD1, MM1 = AK = 2/5 DD1, тогда DM1 = 2/5 DD1 = AK.
BT || KM || AM1, т.е. BT || AM1;
∠M1AD = ∠TBC - острые углы с соответственно параллельными сторонами, AD = BC и ΔADM1 = ΔBCT по катету и острому углу.
Тогда CT = DM1= AK.
AKTC прямоугольник и КТ || AC
KT ⊂ (BMK) следовательно AC || (BMK)
б) (BMK) ∩ (ABC) = QB
DM1 = M1M = 4, AM1 || QM
По т. Фалеса AQ = AD = 8 и ΔQAB - прямоугольный равнобедренный.
Пусть H - середина QB, тогда по свойству равнобедренного треугольника AH ⊥ QB.
Имеем: QB ⊥ AH, QB ⊥ AK, следовательно QB ⊥ (KAH).
В ΔKAH проведём AP ⊥ KH.
Тогда AP ⊥ KH, AP ⊥ QB,
т.е. AP ⊥ (BMK) и AP = AK * AH/KH, искомое расстояние
AH = ½ QB = 4√2.
KH = √AK² + AH² = √16 + 32 = 4√3
AP = 4 * 4√2/4√3 = 4√6/3
ответ: 4√6/3