С. 75
Пошаговое объяснение:
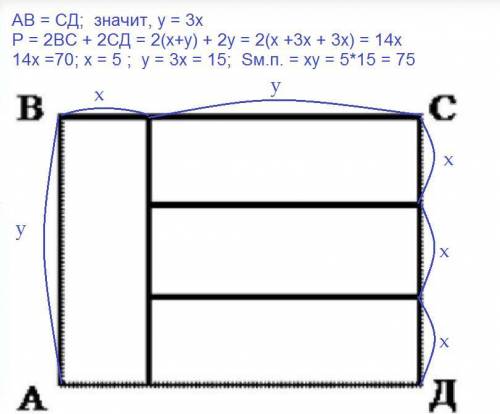
Обозначим меньшую сторону маленького прямоугольника за х, а большую за у.
В большом прямоугольнике АВСD сторона СВ равна у, а сторона СD = 3х; ⇒ у =3х, так как противоположные стороны прямоугольника равны.
ВС = АD = х + у = х + 3х = 4х
Р (АВСD) = 2*( АВ + ВС) = 2 * ( 3х + 4х) = 14х
Так как по условию периметр АВСD равен 10, составим и решим уравнение
14 х = 70
х = 70 : 14
х = 5
у = 3х = 3 * 5 = 15
Площадь маленького прямоугольник равна ху
ху = 5 * 15 = 75
ответ : С. 75
2. Разделите без остатка числитель исходной дроби на ее знаменатель, если она записана в неправильном обыкновенном формате. Если исходное число имеет положительный знак, то полученный результат и будет целой частью. Например, целая часть дроби 716/51 равна 14. Если же исходное число отрицательно, то и здесь от результата следует отнять единицу - например, вычисление целой части дроби -716/51 должно дать число -15.
3. Считайте ноль целой частью положительной дроби, записанной в обыкновенном формате и при этом не являющейся ни смешанной, ни неправильной. Например, это относится к дроби 48/51. Если исходная дробь меньше нуля, то, как и в предыдущих случаях, результат нужно уменьшить на один. Например, целой частью дроби -48/51 следует считать число -1.
4. Отбросьте все знаки, стоящие после десятичной запятой, если выделить целую часть надо из положительного числа, записанного в формате десятичной дроби. В этом случае именно разделительная запятая и отделяет дробную часть от целой. Например, целой частью десятичной дроби 3,14 является число 3. И для этого формата действует определение, согласно которому целая часть не может быть больше исходного числа, поэтому и здесь полученное описанным значение для отрицательного числа надо уменьшать на единицу. Например, целая часть десятичной дроби -3,14 должна быть равна -4.