0.6(2х+6)=(9-х)3.5
1.2х+3.6=31.5-3.5х
1.2х+3.5х=31.5-3.6
4.7х=27.9
х=27.9/4.7
х=5.936
Для дифференцирования понадобится несколько формул:
\begin{gathered}\left( f(x) + g(x) \right)' = f'(x) + g'(x)left( n\cdot f(x) \right)' = n\cdot f'(x)left( x^n \right)' = n \cdot x^{x-1}\end{gathered}
(f(x)+g(x))
′
=f
′
(x)+g
′
(x)
(n⋅f(x))
′
=n⋅f
′
(x)
(x
n
)
′
=n⋅x
x−1
Исходное выражение удобно представить в виде:
F(x) = 3 \sqrt[3]{x^2} - x = 3 x^{2/3} - xF(x)=3
3
x
2
−x=3x
2/3
−x
Продифференцировав его, получаем:
\begin{gathered}F'(x) = (3 x^{2/3} - x)' = (3 x^{2/3})' - (x)' = 3 \cdot \dfrac{2}{3} \cdot x^{2/3 - 1} - 1 = 2\cdot x^{-1/3} - 1 = \dfrac{2}{\sqrt[3]{x}} - 1F'(1) = \dfrac{2}{\sqrt[3]{1}} - 1 = 2 - 1 = 1\end{gathered}
F
′
(x)=(3x
2/3
−x)
′
=(3x
2/3
)
′
−(x)
′
=3⋅
3
2
⋅x
2/3−1
−1=2⋅x
−1/3
−1=
3
x
2
−1
F
′
(1)=
3
1
2
−1=2−1=1
- это та часть поля, которую вспахивает 1-ый тракторист за 1 день, а 
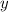- та часть поля, которую вспахивает уже 2-ой тракторист, но тоже за 1 день.Мы можем составить систему уравнений!
За 4 дня первый тракторист вспашет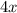
части поля, а второй - 
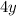части поля. И, по условию, сумма этих двух чисел равна 1 (полю).Время, за которое 1-ый трактор вспашет 
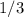поля составляет 
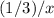, а то время, за которое второй трактор вспашет 
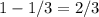поля равно не иначе, как 
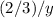. И сумма этих двух отрезков времени - 10 дней.Есть две переменных - но и есть два уравнения:
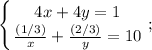
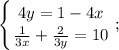
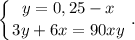
Можем сделать подстановку:
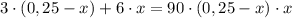
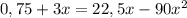
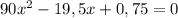
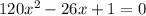
Дальше, воспользовавшись формулой корней полного квадратного уравнения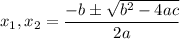 
, получим:
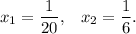
Осталось только 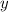-и найти:
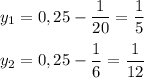
Итак, у нас есть два решения, и между ними придется сделать выбор.
По условию дано, что " ... первый работает медленнее ... ". Это означает, что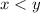 
.
Но под этот критерий подходит только первое решение (так как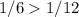 
):
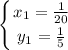
Если мы сделаем проверку, то это решение будет удовлетворять всем условиям.
Но все же заметим, что пока ответа задачи у нас нет. Так что самое время его получить.
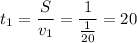(дней)
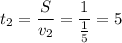(дней)
Задача [наконец] решена!
ответ:первый тракторист может вспахать поле за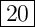 
дней,
а второй - за 
дней.
0.6(2x+6)=(9-x)3.5
1.2х+3.6=31.5-3.5х
1.2х+3.5х=31.3-3.6
4.7х=27.7
х=5.89
тогда как то не красиво получается)