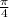
Якому з наведених чисел не може дорівнювати косинус числа? : А) $\frac{\pi }{4}$
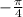
Б) $-\frac{\pi }{4}$
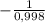
В) $-\frac{1}{0,998}$
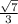
Г) $\frac{\sqrt{7} }{3}$

Question

Математика: Якому з наведених чисел не може дорівнювати косинус числа? : А) Б) В) Г)

lfif123456789 · Accepted Answer

Назовем скорость более медленного поезда «х», а скорость более быстрого поезда «у». Мы знаем это:

y = 1,79x (поскольку скорость одного поезда составляет 79 процентов от скорости другого)

Мы также знаем, что расстояние между поездами уменьшилось на 84 - 58,8 = 25,2 км за 1,5 часа. Мы можем использовать эту информацию, чтобы составить уравнение:

25,2 = 1,5 (у - х)

Мы можем подставить y = 1,79x в это уравнение и решить для x:

25,2 = 1,5 (1,79х - х)

25,2 = 1,5 (0,79х)

х = 21 км/ч

Значит, скорость более медленного поезда равна 21 км/ч, а скорость более быстрого поезда равна:

у = 1,79х = 1,79(21) = 37,59 км/ч

Следовательно, скорость более медленного поезда составляет 21 км/ч, а скорость более быстрого поезда — 37,59 км/ч.

Якому з наведених чисел не може дорівнювати косинус числа? : А) Б) В) Г)

MOGZ ответил

Якому з наведених чисел не може дорівнювати косинус числа? : А) $\frac{\pi }{4}$
Б) $-\frac{\pi }{4}$
В) $-\frac{1}{0,998}$
Г) $\frac{\sqrt{7} }{3}$