Периметр прямоугольника находится по формуле ⇒ P = 2 ( a + b ) , где a - длинна прямоугольника, а b - ширина
Сначала возьмём за a и b самые маленькие значения, то есть 4,5 и 1,8
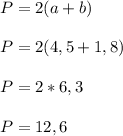
Теперь подставим самые большие значения, то есть 6,2 и 2,5
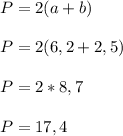
Получается неравенство ⇒ 12,6 ≤ P ≤ 17,4
( Что значит что периметр больше либо равен 12,6 , но меньше либо равен 17,4 )
Площадь прямоугольника находится по формуле ⇒ S = ab , где a - длинна прямоугольника, а b - ширина
Также подставим вместо a и b самые маленькие значения 4,5 и 1,8
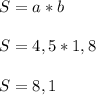
Теперь наибольшие значения 6,2 и 2,5
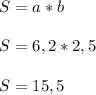
Выходит неравенство ⇒ 8,1 ≤ S ≤ 15,5
( Что значит что площадь прямоугольника больше или равна 8,1 , но меньше либо равна 15,5 )
Позначимо всі значення чисел, які обмежують значення з
1. 7,92 < c < 11,1 .
7--7,92--8з---11---11,1. Дивлячись на схематичне розташування числа с, виходячи з даного нерівності, крайні значення число с приймати не може, так як в знаку нерівності немає значення "або дорівнює". Залишається, що с може приймати такі цілі (натуральні) числа: 8; 9; 10; 11. Це відповідь: з = (8; 9; 10;11.
2. 9 < c < 14,5 аналогічно розташуємо задані числа і виберемо всі цілі значення правіше лівого значення, і лівіше правого.
9--10---с - - - 14--14,5. з = (10; 11; 12; 13; 14).
1) Точка А = 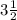 , а точка В =
, а точка В = 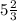 ⇒ расстояние между ними равно В - А
⇒ расстояние между ними равно В - А
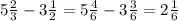
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству 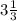 < x < 7
< x < 7
Т.к. 3<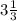 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а) 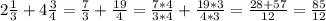
б) 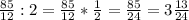
4) Действуем аналогично как в 3 задании
а) 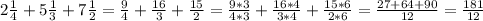
б) 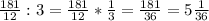
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
Периметр прямоугольника - удвоенная сумма длины и ширины.
Р=2*(а+б)
=>
2*(4,5+1,8) ≤ Р ≤ 2*(6,2+2,5)
2*6,3 ≤ Р ≤ 2*8,7
12,6 ≤ Р ≤ 17,4
Площадь прямоугольника - произведение длины и ширины.
=>
S=а*б
4,5*1,8 ≤ S ≤ 6,2*2,5
8,1 ≤ S ≤ 15,5
Пошаговое объяснение: