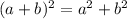 то это большое заблуждение!
то это большое заблуждение!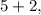 понятно, что
понятно, что 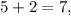 но мы не будем сразу возводить
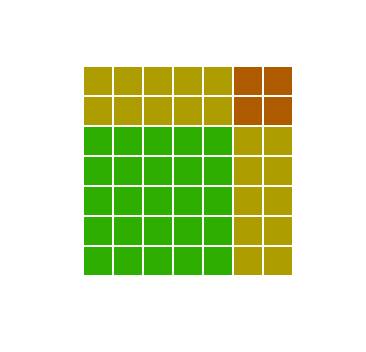
но мы не будем сразу возводить 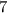 в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)
в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)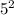 (это зелёный квадрат) и
(это зелёный квадрат) и 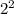 (это оранжевый квадрат), то мы не получим площадь квадрата со стороной
(это оранжевый квадрат), то мы не получим площадь квадрата со стороной 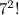 Чтобы получить правильную сумму
Чтобы получить правильную сумму 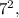 необходимо прибавить ещё два жёлтых прямоугольника с площадями
необходимо прибавить ещё два жёлтых прямоугольника с площадями 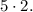
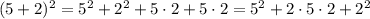 ;
;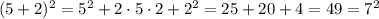 ;
;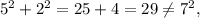 потому:
потому: 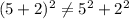 ;
;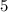 и
и 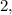 а для каких-то любых
а для каких-то любых  и
и 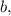 то получилось бы всё аналогично:
то получилось бы всё аналогично: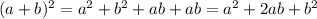 ;
; ;
;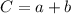 :
: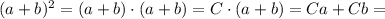
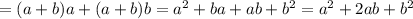 ;
;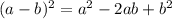 ;
;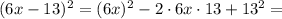
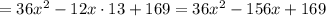 ;
;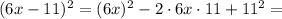
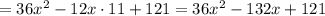 ;
;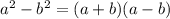 формула [2] ;
формула [2] ;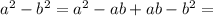
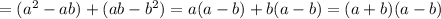 ;
;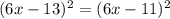 ;
;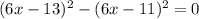 ;
;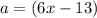 и
и 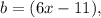 тогда:
тогда: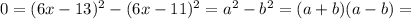
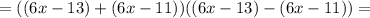
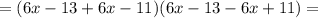
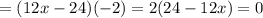 ;
;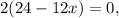 что возможно только если выражение в скобках равна нулю, т.е.:
что возможно только если выражение в скобках равна нулю, т.е.: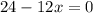 ;
;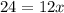 ;
;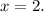
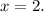
All.
Всего варианто вытащить три карты в такой модели поведения:
Первая 36-стью
Вторая 35-тью
Третья – 34-мя
Всего вариантов упорядоченной выборки – 36*35*34.
I.
Вынуть на первое место бубну можно 9-тью
вынуть на второе место бубну можно 8-мью
вынуть НЕ БУБНУ на третье место можно 27-мью НЕ 34!).
Всего с НЕ-БУБНОЙ на третьем месте.
II.
Вынуть на первое место бубну можно 9-тью
вынуть НЕ БУБНУ на второе место можно 27-мью НЕ 34!),
вынуть на третье место бубну можно 8-мью
Всего с НЕ-БУБНОЙ на втором месте.
III.
Вынуть НЕ БУБНУ на первое место можно 27-мью НЕ 34!),
вынуть на второе место бубну можно 9-тью
вынуть на третье место бубну можно 8-мью
Всего с НЕ-БУБНОЙ на втором месте.
0.
Вынуть на первое место бубну можно 9-тью
вынуть на второе место бубну можно 8-тью
вынуть на третье место бубну можно 7-мью
Всего со всеми бубнами.
Всего подходящих вариантов : 9*8*27 + 9*8*27 + 9*8*27 + 9*8*7 = 9*8*(3*27+7) = 9*8*88
*** было бы ошибкой считать во всех трёх случаях I – III не 27, а 34 и не учитывать отдельно ситуацию [0], так как при этом получилось бы выражение 9*8*102, вместо 9*8*88, поскольку в этом случае были бы посчитаны трижды такие упорядоченные тройки, как, например «Т♦ К♦ Д♦» , когда Д♦ выбрана из 34, либо K♦ выбран из 34, либо Т♦, а две остальные только из бубен.
Итоговая вероятность
При вытаскивании карт рассуждаем в другой модели: вынутые карты кладутся на стол беспорядочно, т.е. тройки «Т♦ К♦ 9♥» , «9♥ Т♦ К♦» и т.п. считаются неразличимыми. Т.е., короче говоря, рассматриваем неупорядоченные тройки.
All.
Всего варианто вытащить три карты в такой модели поведения:
Первая 36-стью
Вторая 35-тью
Третья – 34-мя
И их можно перемешать внутри тройки 6-тью а значит неразличимых вариантов в 6 раз меньше:
Всего вариантов упорядоченной выборки – 36*35*34/6 = 6*35*34.
ДВЕ БУБНЫ
Вынуть на одно из мест бубну можно 9-тью
вынуть на ещё одно из мест бубну можно 8-мью
причём эти места можно поменять местами, значит выбрать пары бубен можно
К ним можно приложить НЕ БУБНУ 27-мью НЕ 34!).
Всего с одной НЕ-БУБНОЙ на одном из мест мест.
ТРИ БУБНЫ
Вынуть на одно из мест бубну можно 9-тью
вынуть на ещё одно из мест бубну можно 8-тью
вынуть на последнее из мест бубну можно 7-мью
И их можно перемешать внутри тройки 6-тью а значит неразличимых вариантов в 6 раз меньше:
Всего со всеми бубнами.
Всего подходящих вариантов : 9*4*27 + 3*4*7 = 3*4*(3*27+7) = 3*4*88
*** было бы ошибкой смешивать случай с двумя и с тремя бубнами, считая третью карту не одной из 27, а сразу одной из 34, так как при этом получилось бы выражение 3*4*102, вместо 3*4*88, поскольку в этом случае были бы посчитаны трижды такие неупорядоченные тройки, как, например «Т♦ К♦ Д♦», когда Т♦ выбран из 34, либо K♦ выбран из 34, либо Д♦, а две остальные из девяти и восьми.
Итоговая вероятность
О т в е т: