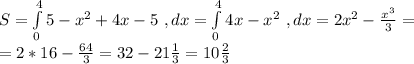y=x²-4x+5 и y=5
y=x^2-4x+5 - парабола у которой ветви направлены вверх
минимум функции при х = 2 и у = 1
Точки пересечения прямой y =5 и параболы
x^2-4x+5 = 5
x^2-4x = 0
x(x-4)=0
x1=0 x2 = 4
Нужно найти площадь под прямой y = 5 и над параболой от x1 = 0 до x2 = 4
S = интеграл (от х1=0 до х2 =4)( 5- x^2+4x-5)dx = интеграл (от х1=0 до х2 =4)( - x^2 +4x)dx = = (-1/3)x^3+2x^2 I(от x1 = 0 до x2 = 4) = (-1/3)*4^3+2*4^2 +(1/3)*0^3 -2*0^2 = -64/3 +32 = 10+2/3 =10,667..
А) 7.300
+
0, 865
8 .165
(3 десятые + 8 десятых = 1 целая , 1 десятая)
Б) 0,3300
-
0,2291
0,1009
(начинаем справа. 0-9=? берём единицу от 3(10-9=1), а где 3 будет 2! 2 ноль. т.к. мы переносили единицу, то вместо нуля будет 9. (9-9=0). 2 (была 3) - 2=0. 3 - 2=1. А целый 0 - 0=0.)
В) 27, 16
*
26
14296
+
5432
6851,16
Г) 1,52
*
3,4
608
+
456
5168
деревьев было посажено в третий день.
Пошаговое объяснение:
Нам известно, что в первый день посадили 30% от общего числа деревьев, то есть от 1200 деревьев; во второй день еще 12% от этого же количества. Приняв 1200 деревьев за 100%, легко найти тот процент деревьев, который был посажен в третий день.
То есть, если в первый и второй день было посажено 30% и 12% соответственно, то в сумме за два дня получаем 42% от 1200 деревьев.
Тогда в третий день было посажено: 100%-42%=58% от 1200 деревьев.
Чтобы найти численное значение определенных процентов от числа, необходимо известное нам значение общего количества деревьев умножить на данную величину процента (в нашем случае, это 58%), и затем поделить на 100: деревьев. - столько деревьев было посажено в третий день, это и будет являться ответом на задачу.
Площади фигур находятся с интеграла
