I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

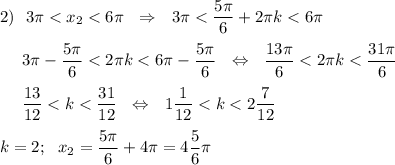
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 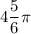
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

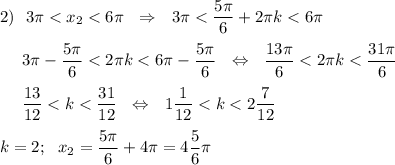
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 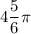
Знаки модулей меняются в точках -4, -5, -6. Вид уравнения получим только на интервалах x>=-4 и x<=-6 (притом второе уравнение тривиально получается из первого). На внутренних отрезках просто найдем координаты концов, а дальше воспользуемся тем, что на отрезках функция линейна.
При x>=-4 все подмодульные выражения положительны, так что y = 2(x + 4) - 3(x + 5) + 3(x + 6) = 2x + 11
При x<=-6 все подмодульные выражения отрицательны, можно просто поменять все знаки:y = -2x - 11
y(-6) = 1
y(-5) = 5
y(-4) = 3
График во вложении.
По этому графику легко определить, при каких k кривая y=kx пересекает данный график ровно в двух точках. Нужные области показаны на рисунке.
Нужные k удовлетворяют неравенствам -3/4<k<-1/6 или -2<k<-1.
Требуемые а, соответственно, в 2 раза меньше.