Пошаговое объяснение:
2 . - 3 1/11 * a *(- 0,11)*b = 34/11 * 11/100 *a*b = 17/50 a*b ;
якщо a*b = 1/17 , то 17/50 a*b = 17/50 * 1/17 = 1/50 = 0,02 .
3 . a) 0,(12 ) = 0,121212... = 0,12 + 0,0012 + ... = 0,12/( 1 - 0,01 ) = 0,12/0,99 = 4/33 ;
б) 1,2(3) = 1,2333... = 1,2 + 0,03 + 0,003 + ... = 1,2 +0,03/(1 - 0,1 ) = 1,2 +3/90 =
= 6/5 + 1/30 = 37/30 .
4 . Нехай вона задумала число х .
Рівняння : х : (- 7 ) - 13,2 = 0,8 ;
х : (- 7 ) = 0,8 + 13,2 ;
х : (- 7 ) = 14 ;
х = 14 * (- 7 ) ;
х = - 98 .
В - дь : число - 98 .
Решение во вложении.
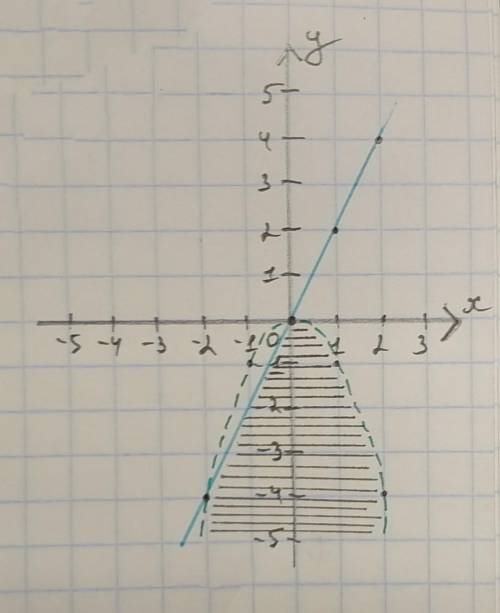
Для решения неравенства грфически вам нужно преобразовать его в функцию f(x)=(...), построить графики данных уравнений, а затем определить, в какой из плоскостей, ограничиваемых графиком, находится нужное множество решений. Для прямой - слева или справа, для параболы - внутри неё или снаружи. Для этого берём любую точку из перечисленных областей и подставляем в неравенство. Если оно верное, зашриховываем выбранную зону. Если нет - противоположную ей область. Для прямой это оказалась область справа от неё, а для параболы - внутри. Затем ищем пересечение штриховок. Это ответ.
Обратите внимание: графическим решением неравенства при строгом знаке (> или <) является ТОЛЬКО определённая вами область, высекаемая графиком. Если знаки нестрогие (<= или >=), то точки самого графика тоже принадлежат множеству решений системы.
Обращаю внимание: я нарисовала новый чертёж с ответом отдельно. Это делать необязательно, достаточно просто хорошо прорисовать область решений на первом чертеже.

2а - первая цифра.
10 • 2а + а - число.
Понятно, что для того, чтобы число было двузначным должно быть:
10 • 2а ≤ 99
а ≤ 99:20
а ≤ 4,95
Следовательно
а = 4 или 3, или 2, или 1
Если при умножении на 19 последняя цифра в результата оказалась равной 5, то значит, на 5 заканчивалось и множимое число.
Если множимое, заканчивающееся на 5 - это результат вычитания из вычитаемого числа 366, то вычитаемое должно заканчиваться на 1.
На 1 заканчивается число, которое было умножено на 7.
Результат умножения на 7 - это:
21,
Значит, на 7 умножалось двузначное число, заканчивающееся на 3.
Итак
3 - последняя цифра.
2•3 = 6 - первая цифра.
6•10 + 3 = 63 - искомое число.
ответ: 63.
Проверка:
1) 63 • 7 = 441
2) 441 - 366 = 75
3) 75 • 19 = 1425 - последняя цифра произведения равна 5.