D(f) = (−∞, 2) или (2, +∞)
Пошаговое объяснение:
Область определения функции — это множество всех значений, которые может принимать переменная 
.
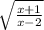может быть как 
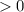, так 
, тут ограничений нет.
А вот подкоренное выражение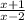 
может быть только 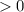, так как квадратный корень из отрицательного числа найти нельзя. Составим неравенство:
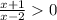
Тут два варианта - либо оба выражения (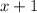 
и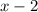 
) , тогда минус на минус даст плюс и конечное выражение 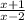будет 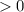, либо оба выражения 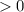. На оба случая составим системы уравнений и решим их:
1.
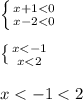можно сократить до просто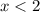 
2.
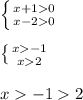можно сократить до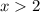 
Также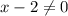 
(или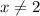 
) т.к. на ноль делить нельзя, но мы никаких корректировок не вносим потому что у нас и так в обоих случаях )
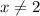И так, конечный ответ:
D(f) = (−∞, 2) или (2, +∞)
Четырехугольник ABCD.
BE = CD = 5
(
с
м
2
)
;
1) AE * BE : 2 = 2 * 5 : 2 = 10 : 2 = 5
(
с
м
2
)
− площадь треугольника ABE;
2) ED * CD = 5 * 5 = 25
(
с
м
2
)
− площадь квадрата EBCD;
3) 5 + 25 = 30
(
с
м
2
)
− площадь четырехугольника ABCD.
ответ: 30
с
м
2
Треугольник KMNF.
1) KF * MF : 2 = 6 * 10 : 2 = 60 : 2 = 30
(
м
2
)
− площадь треугольника KMF;
2) MF * FN : 2 = 10 * 3 : 2 = 30 : 2 = 15
(
м
2
)
− площадь треугольника MFN;
3) 30 + 15 = 45
(
м
2
)
− площадь треугольника KMNF.
ответ: 45
м
2
Четырехугольник PTQR.
1) PX * TX : 2 = 5 * 8 : 2 = 40 : 2 = 20
(
д
м
2
)
− площадь треугольника PTX;
2) TX * XY = 8 * 7 = 56
(
д
м
2
)
− площадь прямоугольника TQXY;
3) QY = TX = 8 (дм);
QY * YR : 2 = 8 * 4 : 2 = 32 : 2 = 16
(
д
м
2
)
− площадь треугольника QYR;
4) 20 + 56 + 16 = 76 + 16 = 92
(
д
м
2
)
− площадь четырехугольника PTQR.
ответ: 92
д
м
2
Пошаговое объяснение:
1) 56/1 : 7/12
56/1 * 12/7 = 8 * 12 = 96 (см) длина
2) S=а*в=96 * 56 = 5376 (см²) площадь прямоугольника
ответ: 5376 см².
Пошаговое объяснение: