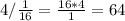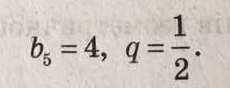
b1=64
Пошаговое объяснение:
b4=b5/q=4÷1/2=8
b3=b2/q=8÷1/2=16
b2=b3/q=16÷1/2=32
b1=b2/q=32÷1/2=64
Высота правильной треугольной пирамида проектируется в центр треугольника. центр правильного треугольника - центр вписанной и описанной окружностей, а также точка пересечения медиан, биссектрис и высот, которые в точке пересечения делятся в отношении 2:1 считая от вершины. высота правильного треугольника вычисляется по формуле: h=a корень 3/2
h=6 корень 3/2. h=3 корень 3
(2/3)*h=2корень3
Прямоугольный треугольник: катет высота пирамиды H(найти), катет (2/3)h, гипотенуза - боковое ребро правильной пирамиды.
по теореме Пифагора:
4²=H²+(2корень3)², Н²=16-12, Н=2
Для наглядности запишем столбиком.
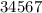
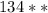
Дальше анализируем.
1) Как обычно, сложение столбиком начинается с последних цифр.
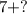(некое однозначное число) = число, оканчивающееся на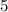 
У нас получится двузначное число (т.к. 8 и 9 - следующие однозначные числа - на 5 не оканчиваются). Ближайшее число - 
.
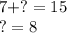
Следовательно, последняя цифра во втором слагаемом будет равна 8.
После первого шага имеем следующую картину:
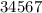
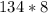
2) Замечаем, что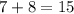 
, следовательно, этот десяток идет в предыдущий разряд в виде единицы (см. правила сложения столбиком).
Тогда в предпоследнем "столбике" (где 6 + * = 8) при сложении нужно учесть эту единицу.
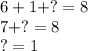
Следовательно, предпоследняя цифра во втором слагаемом = 1.
После второго шага имеем следующую картину:
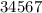
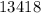
3) Теперь, когда мы имеем первые два числа, можем получить их сумму и заполнить пропуск.
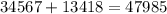
Значит, сумма равна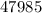 
, и третья пропущенная цифра в ней =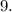 
ответ: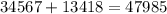
ответ:b₁=64
Пошаговое объяснение:
bₙ=b₁*qⁿ⁻¹
b₅=b₁*q⁴
b₁=b₅/q⁴=