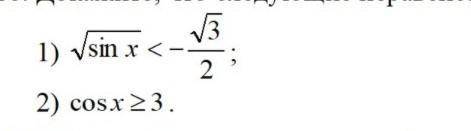
• Давай начнём со второго (он проще):
cos(x) ≥ 3
• Область значений косинуса (E (y)):
-1 ≤ cos(x) ≤ 1 {=} |cos(x)| ≤ 1
Т.е. простыми словами, косинус принимает только эти значения)
Но 3 > 1, ⇒ cos(x) не может быть больше или равен 3,
⇒ cos(x) ≥ 3 - не имеет решений
• Теперь разберёмся с первым
√sin(x) < -√3/2
• Очевидно, что корень из любого действительного числа не может быть меньше отрицательного числа, потому что:
√а ≥ 0
• Отсюда и делаем вывод, что:
√sin(x) < - √3/2 - не имеет решений
Можно лучший ответ?
1) 419; 2) 31440,4
1) (4869484÷1621 + 59058÷18)÷(7560÷504)=419
1) всегда будет в скобках с начало деление потом сложение
4869484÷1621=3004
2) 59058÷18= 3281
3) 3004+3281= 6285
4) потом преступим к другой скобки
7560÷504= 15
5) потом последние действие деление полученного результата с правой и с левой стороны
6285÷15=419
31440 + 1040÷(150 - 2400÷(67 + 53))×20= 31440,4
1) первым действием всегда выполняется в скобках сначала это будет сложение
67 + 53= 120
2) мы будем делить на 2400
2400÷120=20
3) отнимаем от 150
150-20=130
4)130×20=2600
5) 1040÷2600=0,4
6) 31440+0,4= 31440,4
Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
ответ: 8√6 / 3 см3.
1. Квадратный корень по определению положительное число, значит левая часть не может быть меньше отрицательного числа.
2. косинус меняется от -1 до 1, значит не может быть больше либо равен 3.