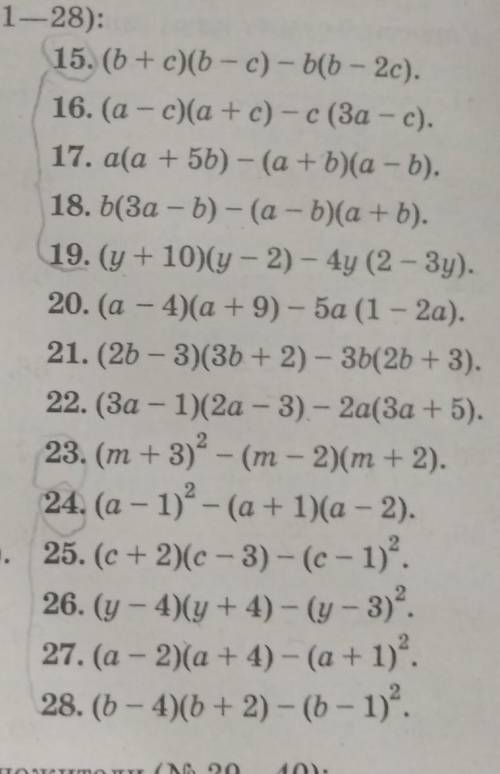
b = 5
i = 3
Пошаговое объяснение:
Необходимо решить уравнение в простых числах:
b+i = (b-i)^3, откуда b-i > 0
Преобразуем уравнение:
(b-i) +2i = (b-i)^3
2i = (b-i)^3 - (b-i)
Рассмотрим общий случай: r ≠ 2; i≠2
А поскольку числа b и i - простые, то это значит, что они нечетные.
Откуда, число b - i является четным, то есть b-i = 2k, где k - натуральное число.
Таким образом:
2i = (2k)^3 - (2k)
2i = 2k( (2k)^2 - 1)
i = k(4k^2 - 1)
Число i является простым, а значит делится только на 1 и на само себя.
Учитывая, что при натуральном k: k <4k^2 - 1, то возможен только один вариант:
k = 1
4k^2 - 1 = i
Откуда:
i = 4*1^2 - 1 = 3 - простое число.
b-i = 2k = 2
b = i + 2 = 5 - простое число
То есть видим одно из решений:
i= 3
b = 5
Рассмотрим теперь случай, когда одно из простых чисел b и i равно 2, но поскольку b>i, то i = 2
2i = (b-i)^3 - (b-i)
4 = (b-2)^3 -(b-2)
b-2 = t - натуральное нечетное число.
t^3 -t - 4 = 0
Откуда t - нечетный делитель числа 4, то есть t =1
1^3 - 1 - 4 ≠ 0
А значит этот вариант отпадает.
Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю,если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь. Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.
Решение.
15. (b + c)(b - c) - b(b - 2c) = b^2 - c^2 - b^2 + 2bc = -c^2 + 2bc
16. (a - c)(a + c) - c(3a - c) = a^2 - c^2 - 3ac + c^2 = a^2 - 3ac
17. a(a + 5b) - (a + b)(a - b) = a^2 + 5ab - (a^2-b^2) = a^2 + 5ab - a^2 + b^2 = 5ab + b^2
18. b(3a - b) - (a - b)(a + b) = 3ab - b^2 - (a^2-b^2) = 3ab - b^2 - a^2 + b^2 = 3ab - a^2
19. (y + 10)(y - 2) - 4y(2 - 3y) = y^2 - 2y + 10y - 20 - 8y + 12y^2 = 13y^2 - 20
20. (a - 4)(a + 9) - 5a(1 - 2a) = a^2 + 9a - 4a - 36 - 5a + 10a^2 = 11a^2 - 36
21. (2b - 3)(3b +2) - 3b(2b+3) = 6b^2 + 4b - 9b - 6 - 6b^2 - 9b = -14b - 6
22. (3a - 1)(2a - 3) - 2a(3a + 5) = 6a^2 - 9a - 2a + 3 - 6a^2 - 10a = -21a + 3
23. (m + 3)^2 - (m - 2)(m + 2) = m^2 + 6m + 9 - (m^2 - 4) = m^2 + 6m + 9 - m^2 +4 = 6m + 13
24. (a - 1)^2 - (a + 1)(a - 2) = a^2 - 2a + 1 - (a^2 - 2a + a - 2) = a^2 - 2a + 1 - a^2 + a + 2 = -a + 3
25. (c + 2)(c - 3) - (c - 1)^2 = c^2 - 3c + 2c - 6 - (c^2 - 2c + 1) = c^2 - 3c + 2c - 6 - c^2 + 2c - 1 = c - 7
26. (y - 4)(y + 4) - (y - 3)^2 = y^2 - 16 - (y^2 - 6y + 9) = y^2 - 16 - y^2 + 6y - 9 = -25 + 6y
27. (a - 2)(a + 4) - (a + 1)^2 = a^2 + 4a - 2a - 8 - (a^2 +2a + 1) = a^2 + 4a - 2a - 8 - a^2 - 2a - 1 = -9
28. (b - 4)(b + 2) - (b - 1)^2 = b^2 + 2b - 4b - 8 - (b^2 - 2b + 1) = b^2 + 2b - 4b - 8 - b^2 + 2b - 1 = 0 - 9 = -9