1) 0,29
2) 0,133
3) 0,09
4) 0,027
все в картинках........-----
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные - машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
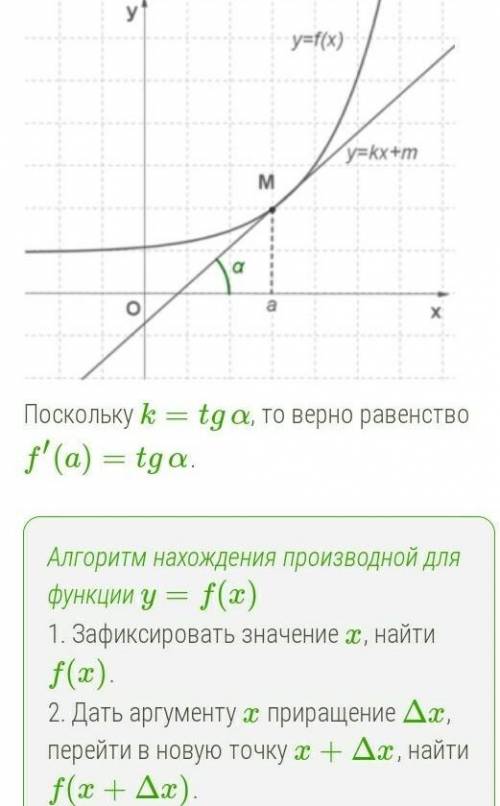
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению - промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.

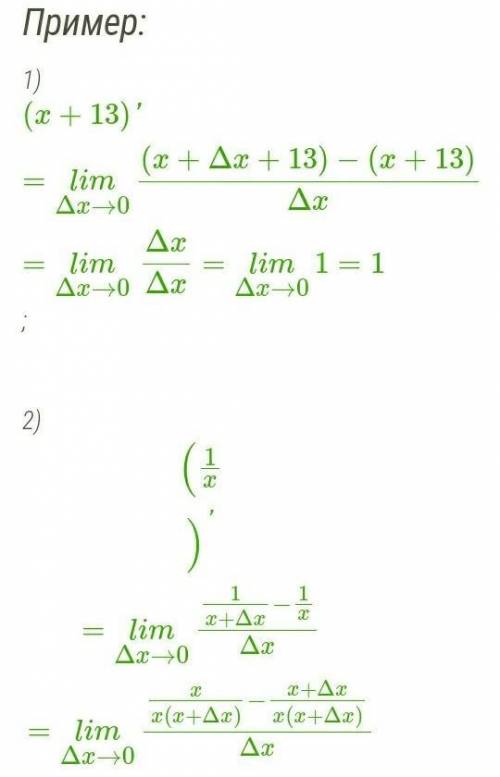


5 5/12+5/6 = 6 1/4
5/6 приводим к знаменателю 12 = 10/12
5 5/12+10/12 = 5 15/12 = 5 5/4 = 6 1/4
1 3/8+7 5/6 = 9 5/24
8/8+3/8 = 11/8
7 5/6 = 42/6+5/6 = 47/6
общий знаменатель - 24
11/8=33/24
47/6 = 188/24
33/24+188/24=221/24 = 9 5/24
5 4/5 - 3 1/5 = 2 3/5
4 3/11 - 5/22 = 4 6/22-5/22 = 4 1/22
8 7/8 - 4 5/6 = 8 21/24 - 4 20/24 = 4 1/24
3) 2 1/5+7/15 = 2 3/15+7/15 = 2 10/15 = 2 2/3
4 8/15+4/9 = 4 24/45+20/45 = 4 44/45
2 6/7-1/7 = 2 5/7
3 5/6 - 1 3/4 = 3 20/24 - 1 18/24 = 2 2/24 = 2 1/12
5 5/12 - 3 3/8 = 5 10/24 - 3 9/24 = 2 1/24
Пошаговое объяснение:
Відповідь:
0,5² +0,2²=0,25+0,04=0,29
0,5³ +0,2³=0,25*0,5+0,04*0,2=0,125+0,008=0,133
(0,5-0,2)² = 0.3²=0.09
(0,5-0,2)³=0.3³=0.027