b {3; -1} ; c {12; 4} ; d {-3; 1}
Пошаговое объяснение:
Коллинеарными называются векторы a и b, координаты которых подчиняются следующему соотношению
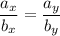
переобозначим вектор MD = a. тогда
Пусть
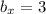
тогда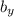 
найдётся из соотношения
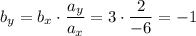
И мы получаем вектор b {3; -1} коллинеарный вектору а {-6; 2) и направленный противоположно.
Найдём ещё один вектор с
Пусть
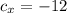
Тогда
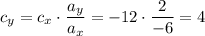
И мы получаем вектор c {12; 4} коллинеарный вектору а {-6; 2} и сонаправленный с ним
Найдём ещё один коллинеарный вектор d
Пусть
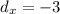
Тогда
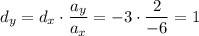
И мы получаем вектор d {-3; 1} коллинеарный вектору а {-6; 2} и сонаправленный с ним.
3) Уравнение медианы АМ.
Координаты точки М найдем по формулам деления отрезка пополам
- точка М.
Уравнение медианы АМ будем искать по формуле для уравнение прямой, проходящей через две заданные точки.
4) Точку пересечения медианы АМ и высоты СН
N(2.4;2.2) - точка пересечения
kason11wd и 104 других пользователей посчитали ответ полезным!
1) уравнение стороны АВ.
Найдем уравнение АВ, проходящей через две заданные точки A и В
2) Уравнение высоты CH
, где (А;B) - направляющий вектор перпендикулярной прямой АВ.
(-3;1) - направляющий вектор.
Пошаговое объяснение:
Пошаговое объяснение:
-3,2x=-6,4
x=-64/(-32)=2
-8x-12=-3x+13
-5x=13+12
x=25/(-5)=-5
-7x=2x+7
-7x-2x=7
x=7/(-9)=-7/9
3(x-2)=-18
x-2=-18/3
x=-6+2=-4