Задача № 8
1) 75-60=15 (с.) - разница.
2) 90: 15=6 (п.) - в одном стеллаже.
3) 75·6=450 (п.) - в I зале.
4) 60·6=360 (п.) или 450-90=360 (п.) - во II зале.
ответ: 450 полок в первом зале и 360 полок во втором зале деткой библиотеки.
Задача № 9
1) 
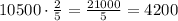(к.) - в учебном разделе.
2) 4 200+1 450=5 650 (к.) - в разделе художественной литературы.
3) 10 500-(4 200+5 650)=10 500-9 850=650 (к.) - в разделе научно-популярной литературы.
ответ: в разделе научно-популярной литературы 650 книг.
Проверка:
4 200+5 650+650=10 500 (к.) - всего.
1) Определим величину угла СВА.
Угол СВА = 180 – АСВ – ВАС = 180 – 35 – 75 = 700.
Так как ВД, по условию, биссектриса угла АВС, то угол СВД = АВД = АВС / 2 = 70 / 2 = 350.
В треугольнике ВСД, угла при основании ВС равны 350, следовательно треугольник ВДС равнобедренный, а ДВ = ДС, что и требовалось доказать.
2) Рассмотрим треугольники ВСД и АВД. В треугольнике АВД угол АДВ = 180 – 30 – 75 = 750.
Треугольники ВСД и АВД равнобедренные с одинаковыми сторонами. ВД = СД = ВД = ВА.
Сравним основания ВС и АД. Основание СД лежит против угла 750, а основание АД против угла 300, следовательно ВС > АД.
ответ: ВС > АД.