Решение
Pascal
Выделить код
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
const
n = 15; {массив из 15 элементов, можно менять}
var
a : array [1..n] of integer;
i, k, ko, _a : integer;
s : real;
begin
s := 0;
k := 0;
ko := 0;
{заполняем и выводим массив, считаем сумму элементов}
writeln('массив:');
randomize;
write('введите A: ');
readln(_a);
for i := 1 to n do
begin
a[i] := random(100) - 50; {создаем i-ый элемент...}
write(a[i], ' '); {...выводим его...}
{если отрицательный суммируем, считаем кол-во}
if a[i] < 0 then
begin
s := s + a[i];
inc(ko)
end;
{если > A и на четном месте количество +1}
if (a[i] > _a) and (i mod 2 = 0) then inc(k)
end;
writeln; {строку перевели}
writeln('среднее арифметическое отрицательных: ', (s/ko):0:6);
writeln('кол-во больших A на нечетных местах: ', k)
end.
Так как 100 делится на все эти числа, то признаком делимости всего числа на данные будет делимость двух последних цифр числа на данные числа:
Делимость на 4 - число из двух последних цифр числа делится на 4.
Делимость на 25 - число из двух последних цифр числа делится на 25.
Делимость на 50 - число из двух последних цифр числа делится на 50.
Делимость на 100 - число оканчивается на 00.
Есл две последние цифры числа нули, то число состоит из целого количества сотен и делится на 4, на 25, на 50 и на 100.
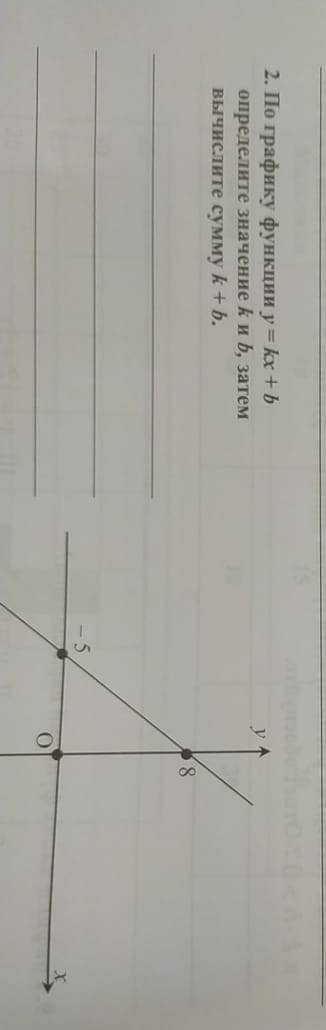
b=8
k+b=9.6
Пошаговое объяснение:
уравнение прямой имеет общий вид y=kx+b, где b - это ордината точки пересечения прямой и осью y (чтобы понять подставь x=0 в уравнение y=kx+b). Отсюда получаем, что k=8.
Вторая точка, которая нам дана с координатами (-5;0), т.е. x=-5 y=0 - подставим в уравнение прямой все известные значения
y=kx+b
0=k*(-5)+8
5k=8
k=1.6
сумма k+b=1.6+8=9.6