обозначим стороны АВ=АС=b, BC=a, биссектрису BL=d,
угол ABL=альфа, тогда углы при основании треугольника ABC=ACB=(2альфа)
угол при вершине BAC=(180-4альфа)
и альфа должен быть < 45 градусов, т.е. 2альфа должен быть < 90 градусов, т.к. в равнобедренном треугольнике угол при основании не может быть тупым...
угол ALB=(3альфа)
по т.синусов: a*sin(2альфа) = b*sin(180-4альфа)
отсюда a = b*sin(180-4альфа) / sin(2альфа) = b*sin(4альфа) / sin(2альфа) =
= 2*b*cos(2альфа)
по т.синусов: AL*sin(3альфа) = b*sin(альфа)= 2*b*cos(2альфа)
по т.синусов: AL*sin(3альфа) = b*sin(альфа)
по условию задачи d = BC - AL = a - b*sin(альфа) / sin(3альфа) =
= 2*b*cos(2альфа) - b*sin(альфа) / sin(3альфа) = = b* ( 2*cos(2альфа) - sin(альфа) / sin(3альфа) )
для длины биссектрисы справедлива формула: d = 2*a*b*cos(альфа) / (a+b)
отдельно запишем a+b = 2*b*cos(2альфа) + b = b*(2*cos(2альфа) + 1)d = 2*2*b*cos(2альфа)*b*cos(альфа) / ( b*(2*cos(2альфа) + 1) ) =
=4*b*cos(2альфа)*cos(альфа) / (2*cos(2альфа) + 1)
если приравнять два получившихся равенства для биссектрисы d, то длина стороны b сократится и останется тригонометрическое равенство:
sin(альфа) / sin(3альфа) =
= 2*cos(2альфа) - 4*cos(2альфа)*cos(альфа) / (2*cos(2альфа) + 1)после несложных преобразований можно получить равенство:
2*cos(2альфа)*(4*(cos(альфа))^2 - 1) = 1 + 4*cos(2альфа)*cos(альфа)
это выражение можно привести к полному уравнению четвертой степени относительно косинуса альфа (но у меня красивое решение этого уравнения никак не получается...)))одно из решений здесь очевидно... cos(альфа) = +- 1/2
но этот угол не может быть в равнобедренном треугольнике (см. выше...)))
если решать оставшееся кубическое уравнение, то единственным подходящим решением получается cos(альфа) =примерно= 0.94 (0.93969)
это угол около 20 градусов
тогда углы данного равнобедренного треугольника 40, 40, 100
найдём координаты и длину вектора:
= (5,2,0),
найдем угол между ребрами А1А2 и А1А4.
Для этого найдём координаты и длину вектора :
= (1,2,4),
Векторное произведение векторов: и :
;
угол между ребром А1А4 и гранью А1А2А3
найдем каноническое уравнение ребра А1А4
,
– каноническое уравнение ребра А1А4
Найдем уравнение плоскости, проходящей через точки
А1(2,4,3), А2(7,6,3), А3(4,9,3):
уравнение плоскости, проходящей через точки А1, А2, А3:
Синус угла между ребром А1А4 и гранью А1А2А3
площадь грани А1А2А3;
Грань А1А2А3 – это треугольник, площадь которого равна ? площади параллелограмма, построенного на векторах и
= (5,2,0),
= (2,5,0),
Векторное произведение векторов:
Находим площадь треугольника А1А2А3:
5) объём пирамиды;
= (5,2,0),
= (2,5,0),
= (1,2,4),
Смешанное произведение векторов:
объём пирамиды
6) уравнения прямой А1А2;
а). Как пересечение двух плоскостей А1А2А3 и А1А2А4:
уравнение плоскости, проходящей через точки А1, А2, А3:
Найдем уравнение плоскости, проходящей через точки
А1(2,4,3), А2(7,6,3), А4(3,6,7):
уравнение плоскости, проходящей через точки А1, А2, А4:
Общие уравнения прямой А1А2:
б). каноническое уравнение прямой А1А2:
,
– каноническое уравнение ребра А1А2
с). параметрическое уравнение прямой А1А2:
7) уравнение плоскости А1А2А3;
А1(2,4,3), А2(7,6,3), А3(4,9,3):
уравнение плоскости, проходящей через точки А1, А2, А3:
8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3.
уравнение плоскости, проходящей через точки А1, А2, А3:
Нормальный вектор данной плоскости
Уравнение высоты А4Н, опущенной из т. А4(3,6,7) на плоскость А1А2А3, имеет вид:
Найдем координаты т.Н:
Решая параметрическое уравнение прямой А4Н
и уравнение плоскости А1А2А3: , имеем: , отсюда координаты т.Н.
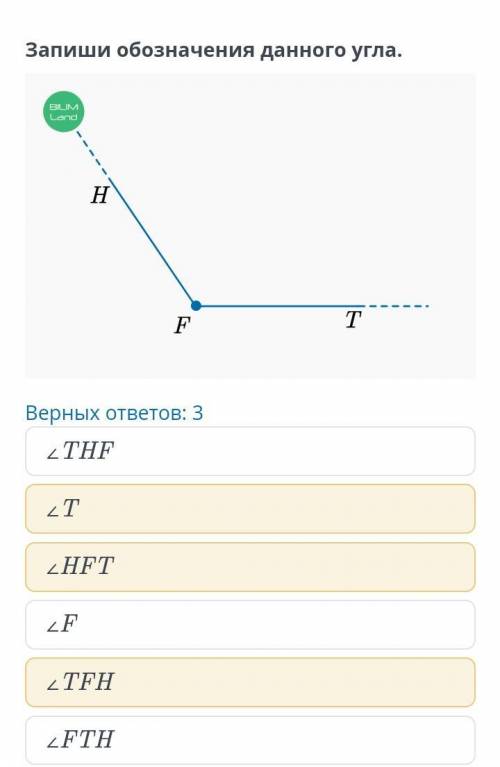
1) НFT
2)TFH
3) точно не знаю,
но неправильно THF, T, FTH
остается уголF ?