
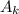 (т.е. вероятность того, что произойдёт в точности
(т.е. вероятность того, что произойдёт в точности 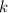 успехов из
успехов из 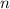 ), подчиняется биномиальному распределению:
), подчиняется биномиальному распределению: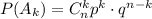 , где
, где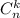 означает число выбрать из
означает число выбрать из 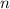 элементов
элементов 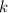 элементов без учёта порядка. Известно, что
элементов без учёта порядка. Известно, что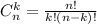 .
.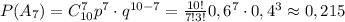
 состоит из двух непересекающихся множеств-альтернатив:
состоит из двух непересекающихся множеств-альтернатив: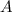 - есть хотя бы одно попадание;
- есть хотя бы одно попадание;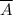 - нет ни одного попадания.
- нет ни одного попадания.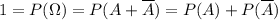 , поэтому интересующая нас вероятность выражается следующим равенством:
, поэтому интересующая нас вероятность выражается следующим равенством: 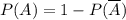 .
.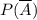 . Можно действовать по общей формуле вероятностей в схеме испытания Бернулли (и получить тот же самый результат!), но в данном случае ситуация упрощается, если напрямую воспользоваться независимостью испытаний: вероятность непопадания в серии из 10 выстрелов равна произведению вероятностей непопадания после 1-го выстрела, после 2-го выстрела и т.д., до 10-го выстрела:
. Можно действовать по общей формуле вероятностей в схеме испытания Бернулли (и получить тот же самый результат!), но в данном случае ситуация упрощается, если напрямую воспользоваться независимостью испытаний: вероятность непопадания в серии из 10 выстрелов равна произведению вероятностей непопадания после 1-го выстрела, после 2-го выстрела и т.д., до 10-го выстрела: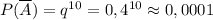 ,
,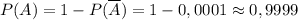
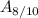 "не менее 8-ми пуль попали в цель" является суммой трёх взаимоисключающих событий
"не менее 8-ми пуль попали в цель" является суммой трёх взаимоисключающих событий 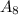 "ровно 8 из 10 пуль попали в цель",
"ровно 8 из 10 пуль попали в цель", 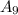 "ровно 9 из 10 пуль попали в цель" и
"ровно 9 из 10 пуль попали в цель" и 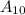 "ровно 10 из 10 пуль попали в цель", поэтому искомая вероятность равна:
"ровно 10 из 10 пуль попали в цель", поэтому искомая вероятность равна: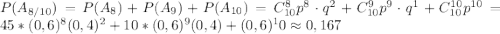
Сначала выберем каких-нибудь троих красных хамелеонов. Так как они все не сидят на одной прямой, они сидят в вершинах треугольника. Пусть данный треугольник не удовлетворяет условию задачи, тогда на его сторонах есть хотя бы три синих хамелеона. Так как эти три синих хамелеона не сидят на одной прямой, они сидят в вершинах треугольника, площадь которого меньше площади предыдущего. Если новый треугольник снова не удовлетворяет условию задачи, выберем аналогичным образом (на сторонах нового треугольника) ещё один. Так как каждый последующий треугольник по площади меньше предыдущего, когда-нибудь этот процесс остановится. Полученный в конце треугольник удовлетворяет условию задачи.