507. Дано: ΔABC, CH і AT — висоти, AB = 8 см, ВС = 6 см, СН = 3 см. Знайти АТ.
Площа трикутника рівна половині добутку сторони на висоту, проведену на цю сторону.
Знайдемо площу трикутника ΔABC:
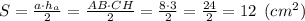
Виразимо іншу висоту через цю ж формулу:
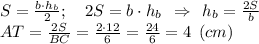
Відповідь: АТ = 4 см.
508. Дано: ΔEFS — рівнобедрений, EF — основа, EF = 40 см, SF = 29 см. Знайти S(EFS).
SF = SE = 29 см, так як ΔEFS — рівнобедрений.
Проведемо висоту SH до основи тр-ка. Висота у рівнобедреному тр-ку є медіаною, тому EH = FH = 40/2 = 20 см.
Знайдемо катет SH з ΔESH (∠EHS = 90°) за т. Піфагора:
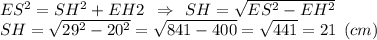
Підставимо значення у формулу площі трикутрина:
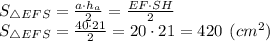
Відповідь: Площа ΔEFS рівна 420 см².

1) 12143+11778=23921.
2) 8*24372=194976.
3) 23921*7=167447.
4) 194976-167447=27529.
2) 100*(11372-10599)*6+19060*4=540040.
1) 11372-10599=773.
2) 100*773=77300.
3) 77300*6=463800.
4) 19060*4=76240.
5) 463800+76240=540040.
3)(24372 - 3979) * 8 + 90 * 10 : 5=20573
1)24372-3979=20393
2)20393*8=163144
3)90*10=900
4)900:5=180
5)20393+180=20573
4)180:12*1000-906:3+3007*2=20712 1) 180:12=15. 2) 15*1000=15000. 3) 906:3=302. 4) 3007*2=6014. 5) 15000-302=14698. 6) 14698+6014=20712