Задача №1
Спортсмен бежит дистанцию 3 км. ему осталось пробежать 1650 м. сколько метров спортсмен уже пробежал?
Краткое условие:
Всего - 3км
Пробежал - ?
Осталось - 1650 м
1 км = 1000 м
1. 1000 * 3 = 3000 (м) - длина всей дистанции
2. 3000 - 1650 = 1350(м) - пробежал спортсмен
ответ: 1350
Задание №2
Найди значение выражения 45 045 : 15 - 240 * 5 + 200 Запиши решение и ответ.
45 045 : 15 - 240 * 5 + 200 = 2003
1. 45045 : 15 = 3003
2. 240 * 5 = 1200
3. 3003 - 1200 = 1803
4. 1803 + 200 = 2003
Задание №3
Андрей купил три банки кабачковой икры. В каждой банке 530 г. икры. Стеклянная банка весит 260 г. Сколько граммов весит вся икра вместе с банками?
Краткое условие:
Всего - 3 банки икры
Вес банки - 260 г.
Вес икры - 530 г.
Вес всей икры с банками - ?
1. 530 + 260 = 790 (г) - вес 1-ой банки с икрой
2. 790 * 3 = 2370 (г) - вес всей икры вместе с банками
ответ: 2370
Задание №4
Аня написала своё имя красками на альбоме,закрыла альбом,краска не высохла и отпечаталась на второй половинке альбома нарисуй(напиши) что увидела Аня когда открыла альбом.
Аня написала свои имя в альбоме. Закрыв его, изображение не успело высохнуть и отпечаталось на соседнем листке в зеркальном виде. Получается, что из имени АНЯ получилось RНА.
ответ: RНА
Задание №5
В волшебной стране шесть деревень и один замок.Замок соединён дорогами со всеми деревнями . Каждая деревня соединена с тремя соседними. Других дорог в волшебной стране нет. Сколько всего дорог в волшебной стране?
1. 6*3 = 18 (дорог) - нужно, чтобы соединить деревни с тремя соседними
2. 18 : 2 = 9 (дорог) - так как каждая дорога посчитана дважды
3. 9 + 6 = 15 (дорог) - всего
ответ: 15
1)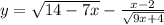
Область определения этой функции должна удовлетворять двум условиям:
1) подкоренное выражение неотрицательно (т.е. 14 - 7х ≥ 0 и 9х + 4 ≥ 0)
2) знаменатель дроби отличен от нуля (т.е. )
)
Поэтому эти условия удобно записать в виде системы:
Решением системы неравенств будет множество, которое и есть область определения функции.
ответ:![(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/39742.png)
2) Рисунок к задаче - во вложении.
Проведем отрезки BD и AC.
Получим, что ΔABD=ΔCDB по трем сторонам (BD-общая, CB=AD, CD=AB) и ΔCDA=ΔABC по трем сторонам (AC-общая, CB=AD, CD=AB).
Из равенства ΔABD и ΔCDB следует, что соответственно равны ∠A и ∠C.
А из равенства ΔCDA и ΔABC следует, что соответственно равны ∠D и ∠B.
Наконец, рассмотрим ΔCOB и ΔAOD. У них CB=AD, ∠A=∠C, ∠В=∠D. Значит, ΔCOB = ΔAOD по стороне и прилежащим к ней углам.
Из равенства ΔCOB и ΔAOD следует равенство соответственных сторон СО и AO.
Доказано.