ДАНО
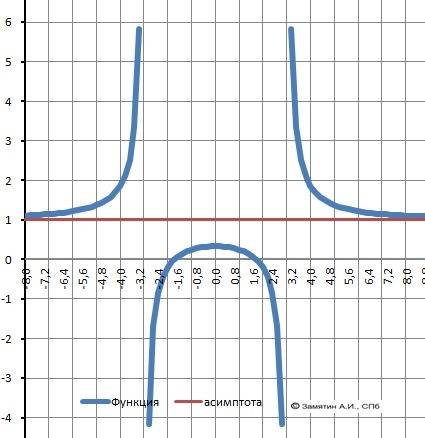
Y= (x²-3)/(x²-9)
ИССЛЕДОВАНИЕ
1.Область определения D(x): В знаменателе (x²-9)=(x-3)(x+3)≠0.
Х∈(-∞;-√3))∪(√3;+∞). Две точки разрыва.
Вертикальные асимптоты: х = -√3 и x = √3.
2. Пересечение с осью Х. Y=0. (х²- 3)=0. X1=-√3, X2= +√3.
3. Пересечение с осью У. У(0) = 3/9 = 1/3.
4. Поведение в точках разрыва.
limY(-√3-) =+ ∞, limY(-√3+) =-∞,limY(√3-) =-∞, limY(√3+) = +∞.
5. Исследование на чётность.Y(-x) = Y(x). Функция чётная.
6. Производная функции -Y'(x).
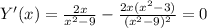
Корень при х=0.
7. Локальный экстремум. Максимум Ymax(0)= 1/3.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-√3)∪(-√3;0] , убывает = Х∈[0;√3)∪ (√3;+∞).
8. Вторая производная - Y"(x) - без расчета.
Точек перегиба - нет.
Выпуклая “горка» Х∈(-√3;√3), Вогнутая – «ложка» Х∈(-∞;-√3)∪ (√3;+∞)
10. Горизонтальная асимптота
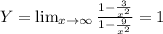
12. График в приложении.
На каждой полке по 9 ячеек, поэтому
y = 9(x-1) + a; a ∈ [1; 9]
Тогда номер полки Блестюши тоже y, а номер ячейки z.
z = 9(y-1) + b; b ∈ [1; 9]
Сумма номеров ячеек y + z = 777
9(x-1) + 9(y-1) + a + b = 777 = 9*86 + 3
Очевидно, что остатки a + b > 3, то есть a + b = 9 + 3 = 12, тогда
9(x - 1 + y - 1) = 9*85
x + y - 2 = 85
x + y = 87
Подставим в 1 уравнение
y = 9(x - 1) + a
87 - x = 9x - 9 + a
96 = 10x + a; x = 9; a = 6; тогда y = 9*8 + 6 = 78
z = 9*77 + b = 693 + b
С другой стороны,
y + z = 777
z = 777 - y = 777 - 78 = 699 = 693 + b; тогда b = 699 - 693 = 6
Номер полки Звездочки: x = 9; номер ячейки y = 78.
Номер полки Блестюши y = 78, номер ячейки z = 699.