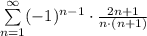
Исследуем этот ряд на абсолютную сходимость.
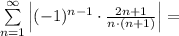
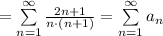
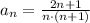
Рассмотрим ряд
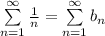
Используем предельный признак сравнения:
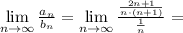
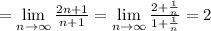
Значит ряды 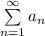 и
и 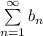
сходятся или расходятся одновременно, но ряд
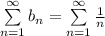
это гармонический ряд, который расходится. Значит и ряд
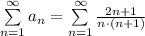
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
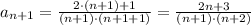
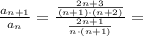
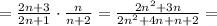
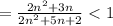
т.к. 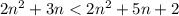 ⇔
⇔ 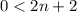 ⇔
⇔ 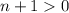 .
.
То есть 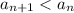 .
.
То есть последовательность 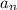 монотонно убвывает.
монотонно убвывает.
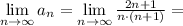
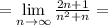
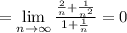
То есть последовательность 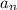 монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
Відповідь:
Покрокове пояснення:
1. За схемою Бернуллі
р=0.8
q=1-p=0.2
n=20
np-q=<m=<np+p
20×0.8-0.2=<m=<20×0.8+0.8
15.8=<m=<16.8
найімовірніше вийде з ладу протягом року 16 лампочок
2. Із 6 ящиків відкладемо зразу для 8 поверху
Маємо 6 ящиків ●●●●●●
Між ними треба поставити риски-роздільники між поверхами
●●●●|●●|
Але між останніми рисками повинно бути 2 ящика, тому 7 рисок розтавляємо між 4 ящиками
Наприклад
|●| |●| | |●●| |●● |
1 ящик доставлено на перший та третій поверхи, два на 6 поверх та маємо 2 на 8 поверсі
Всього маємо 11 (4+8-1) елементів, які треба упорядкувати, крайні не переставляємо, тому маємо
С ів
Так як ящики різні, то їх можна упорядкувати
Всього 330×6!