ответить
Т.к.BD:CD=1:2(т.к.биссектриса), AB:AC=1:2, BK- медиана, то (.) K делит АС пополам, то AB=AK, то треугольник KAB- равнобедренный и его биссектриса AE является ещё и медианой.=> BE=EK.По свойству медианы это значит,что S треугольников ABE и AEK равны и S ABK и BKC равны.Т.к. AD - биссектриса, делящая BC в отношении 1:2, то S ABD относится к S ADC так же как и 1:2.Т.к. S ABC=60,то S треугольников ABK и BKC=30(каждый треугольник), а ABD и ADC равны 20 и 40.
Пусть х- S искомого четырехугольника,тогда S BED= 30-х,S ABE= S ABD - S BED = 20-(30-х) = х-10, но S AEK такая же, так как они равны с BED.Но S ADC = 40 = S AEK + S EDCK = x-10+x=2x-10 =40. х = 25.
ответ: S EDCK=25.
y = -x-6
Пошаговое объяснение:
Касательная является параллельной другой прямой, если углы их наклона совпадают.
Если Вам известно понятие производной функции в точке, то можно использовать её геометрический смысл: производная в точке равна тангенсу угла наклона касательной в данной точке.
Так, например, наклон функции y=-x+2 одинаков во всех точках и равен -1, т.е. y' = -1.
Необходимо найти такие точки, принадлежащие y=x+2/x-2, в которых производная этой функции была бы равна -1.
Найдём производную: y' = 1 - 2/x^2.
Приравняем производную к -1: 1 - 2/x^2 = -1;
Отсюда следует, что x = ±1 -- это абсциссы точек, в которых производная функции равна -1.
Значения y для этих точек 1 и -5, т.е. точки (1, 1) и (-1, -5).
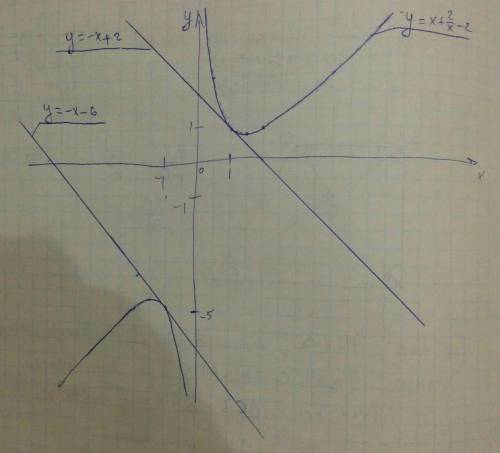
Касательной к графику функции y = x+2/x-2 в точке (1, 1) является прямая y = -x + 2, которая задана в условии. В точке (-1, -5) касательной является прямая y = -x - 6.
Если Вам неизвестно понятие производной, то просто постройте график данных функций и найдите экспериментально линейкой ту точку, в которой касательная будет параллельна y = -x + 2.
Построение в приложении.
x>3
Является, т.к. x - положительное число и больше вычитаемого.