
S = 52 см
Ширина = 4 см
52 / 4 = 13 см
ответ: 13 см
Решим задачу на расстояние, время, скорость
Дано:
t(пр. теч.)=3 ч
t(по теч.)=2 ч
v(собств.)=18,6 км/час
v(теч.)=1,3 км/час
S=? км
Решение
1) Чтобы найти расстояние, которое катер проплыл против течения, нужно найти скорость катера против течения:
v(пр. теч.)=v(собств.) - v(теч.)=18,6 - 1,3 = 17,3 (км/час)
2) Расстояние против течения равно:
S(расстояние)=v(скорость)×t(время)
S(пр. теч.)=v(пр. теч.)×t(пр. теч.)=17,3×3= 51,9 (км)
3) Чтобы найти расстояние, которое катер проплыл по течению, нужно найти скорость катера по течению:
v(по теч.)=v(собств.) + v(теч.)=18,6 + 1,3 = 19,9 (км/час)
4) Расстояние по течению равно:
S(по теч.)=v(по теч.)×t(по теч.)=19,9×2=39,8 (км)
5) Путь, который катер равен:
S=S(пр. теч.)+S(по теч.)=51,9+39,8= 91,7 (км)
ОТВЕТ: катер путь 91,7 км.
1,2*840 = 1008 км - пролетел сначала
0,6*780 = 468 км - пролетел еще
468+1008 = 1476 км пролетел всего
1,2+0,6=1,8 часа - время полета
1476:1,8 = 820 км/ч - средняя скорость
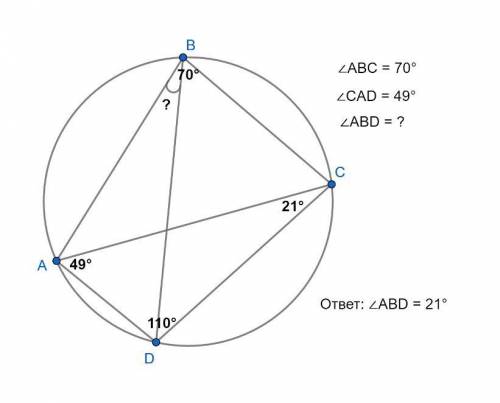
∠ABD = 21°.
Пошаговое объяснение:
Рисунок прилагается.
Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 180°.
∠ABC + ∠ADC = 180° ; ∠ABC = 70° по условию.
∠ADC = 180° - ∠ABC = 180° - 70° = 110°;
Сумма углов треугольника = 180°. В ΔCAD ∠CAD = 49° по условию, ∠ADC = 110°; ∠ACD = 180° - ∠CAD - ∠ADC = 180° - 49° - 110° = 21°.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны между собой.
∠ABD и ∠ACD вписанные углы, опирающиеся на одну хорду AD.
∠ABD = ∠ACD = 21°.
a-длина
a=S/ширина
a=52/4=13cm