Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 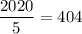 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 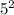 :
:
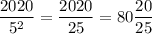
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 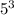 :
:
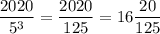
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 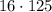 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 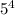 :
:
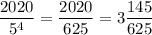
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 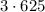 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 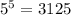 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
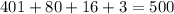
Значит, число 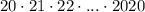 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 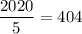 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 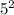 :
:
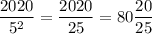
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 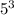 :
:
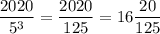
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 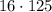 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 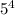 :
:
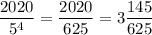
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 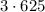 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 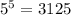 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
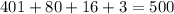
Значит, число 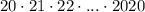 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
f:80=600-400 обозначает проверка.
f:80=200
f=200*80
f=16000
400+16000:80=400+200=600
600=600
ответ:f=16000
2)500*x-600=400
500х=600+400
500х=1000
х=1000:500
х=2
500*2-600=400
400=400
ответ:х=2
3)1300-(b+800)=400
b+800=1300-400
b+800=900
b=900-800
b=100
1300-(100+800)=1300-900=400
400=400
ответ:b=100
4)600*20-n=60
12000-n=60
n=12000-60
n=11940
600*20-11940=60
60=60
ответ:n=11940
Можешь списывать спокойно!Уравнения решены правень, так как равнения всегда решаю хорошо и правильно!Видишь, даже ответы с проверкой одинаковые!В правом верхнем углу я написала обозначения.Если, что то можешьпеределать по своему кк вы решаете в школе.
Надеюсь, что з