Моторная лодка проплыла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 10 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 5 км/ч. ответ дайте в км/ч.
ответ: 11
* Пусть скорость лодки в неподвижной воде равна X км/ч.
* Решаем по формуле s = v * t.
* t = s / v
S - путь V - Скорость t - время По течению: 96 км (x + 5) км/ч (96 / x + 5 ) ч Против течения 96 км (x - 5) км/ч (96 / x - 5) чПо условию задачи известно, что на путь по течению лодка затратила 10 часов меньше, чем против течения, составим уравнение:
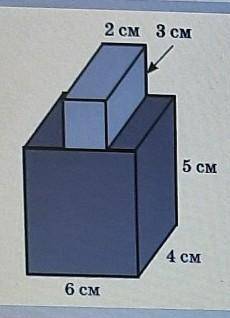
184 см²
Пошаговое объяснение:
Площадь поверхности тёмно-синего параллелепипеда равна
S₁ = 2 · (6 · 5) + 2 · (4 · 5 ) + 2 · (6 · 4) - 2 · 4 = 140 (cм²)
Площадь поверхности светло-синего параллелепипеда равна
S₂ = 2 · (2 · 3) + 2 · (4 · 3 ) + 2 · (2 · 4) - 2 · 4 = 44 (cм²)
Площадь полной поверхности детали
S = S₁ + S₂ = 140 + 44 = 184 (см²)