Пошаговое объяснение:
Разобьём всех гномов по тройкам, чтобы найти сколько из них могут стоять между гномами в колпаках одного цвета:
105:3=35, а нужно 67. Значит надо добавить к 32 тройкам по гному в таком же колпаке. Получается 32 квартета одного цвета и 3 тройки:
3×3+32×4=137.
31 гном лишний, т. е. 8 квартетов подряд должны быть одного цвета. Остаётся 16 квартетов и 3 тройки, из которых две соседние тройки должны быть одного цвета. Итак имеем 8 соседних квартетов одного цвета, 2 соседних тройки одного цвета, а также 16 квартетов и тройка разных цветов. Или всего имеем 27 наборов разных цветов. Если разместить их по кругу, то первый и последний наборы должны быть разных цветов. То есть красных наборов может быть (27-1):2=13. С каждой стороны красных наборов будут не красные наборы. Таким образом максимум 26 гномов в красных колпаках могут иметь соседа не в красном колпаке.
Задачу можно интерпретировать как 250 опытов с фиксированной вероятностью успеха и неудачи в каждом отдельном испытании, т.е. по факту мы имеем биномиальное распределение, применима формула Бернулли
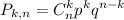
или в нашем случае
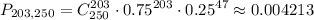
Если мощного калькулятора под рукой нет, то лучше вместо биномиального использовать нормальное распределение. Это допустимо, ведь из центральной предельной теоремы следует что при неограниченном возрастании числа опытов ф-я распределения будет неограниченно приближаться к нормальному распределению (с мат. ожиданием 0 и дисперсией 1)
Пошаговое объяснение:
-0,6*a+1*a=a*(-0,6+1)=0,4*a
По сути мы выносим за скобки общий множитель а.
Если вы складываете 2а+3а, например, то выполняете тоже действие
а*(2+3)=5а, только делаете это в уме.
Аналогично и с вычитанием, ну или как в вашем примере, один из сомножителей со знаком минус.