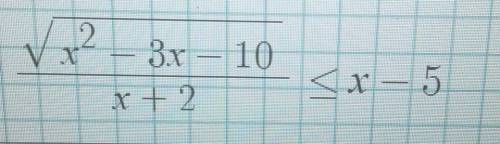
Верно рассуждение 1
Пошаговое объяснение:
Рассуждение 1 верно: действительно, есть всего 8 возможных вариантов, как поставить корабль. Если сделать 8 выстрелов, выбрав по одной клетке, входящей в каждый вариант, то хотя бы раз мы гарантированно попадем.
Рассуждение 2 неверно: разные положения корабля пересекаются, поэтому одним выстрелом можно проверить сразу несколько возможных положений.
Рассуждение 3 неверно: показано, что если из последовательности выстрелов по диагонали убрать какой-то выстрел, то можно поставить корабль так, чтобы в него не попали. Из этого следует, что если стрелять по диагонали, то нужно сделать 4 выстрела, но не следует, что если стрелять как-то еще, то по-прежнему нужны все 4 выстрела.
На саму задачу, конечно, ответ 4: достаточно выстрелить на все клетки по диагонали, если корабль стоит в i-й горизонтали или i-й вертикали, то на i-м выстреле мы его подобьем. Меньшим количеством выстрелов обойтись нельзя: рассмотрим все вертикали, в которых стоят клетки, по которым выстрелили. Если выстрелов меньше 4, то и вертикалей меньше 4, можно выбрать вертикаль, по которой еще не стреляли, и поставить туда корабль.
х=<1,5-0,5*sqrt(53) или x>=1,5+0,5*sqrt(53) или х=5
Пошаговое объяснение:
Подкоренное выражение (х-5)*(х+2)
ОДЗ х>=5 или x<-2
Если х>5, то неравенство эквивалентно:
sqrt(x-5)*sqrt(x-2)>=1
или х^2-3x-10>=1
х^2-3x+2,25>=13,25
(x-1,5)^2>=(0,5*sqrt(53))^2
с учетом ОДЗ
x>=1,5+0,5*sqrt(53)
Если x<-2 точно также приходим к
x<=1,5-0,5*sqrt(53)
Если х=5, то неравенство превращается в равенство, так, что это решение.